Menu Close

Solve-the-equation-z-2-2-1-j-z-2-0-Givin-each-result-in-form-a-jb-with-a-and-b-correct-to-2dp-

Tinku Tara 0 Comments
Pin




Question Number 15348 by tawa tawa last updated on 09/Jun/17
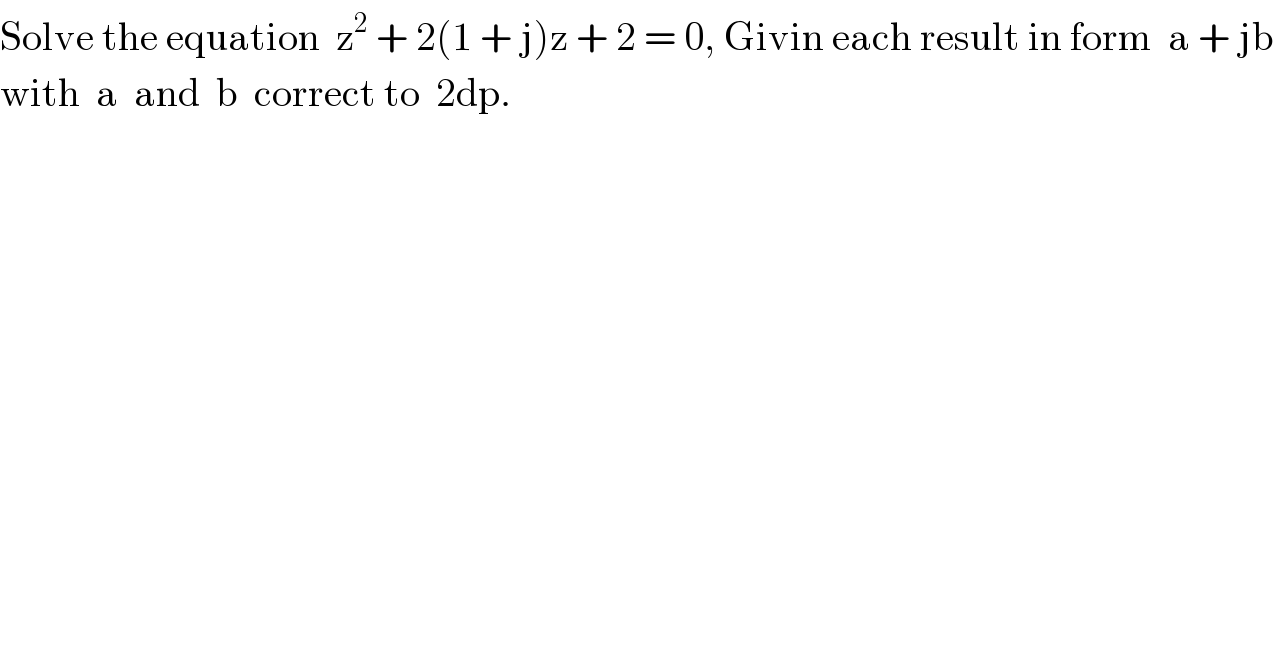
Solve the equation z^2 + 2(1 + j)z + 2 = 0, Givin each result in form a + jb with a and b correct to 2dp.
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\:\:\mathrm{z}^{\mathrm{2}} \:+\:\mathrm{2}\left(\mathrm{1}\:+\:\mathrm{j}\right)\mathrm{z}\:+\:\mathrm{2}\:=\:\mathrm{0},\:\mathrm{Givin}\:\mathrm{each}\:\mathrm{result}\:\mathrm{in}\:\mathrm{form}\:\:\mathrm{a}\:+\:\mathrm{jb} \\ $$$$\mathrm{with}\:\:\mathrm{a}\:\:\mathrm{and}\:\:\mathrm{b}\:\:\mathrm{correct}\:\mathrm{to}\:\:\mathrm{2dp}. \\ $$
Answered by RasheedSoomro last updated on 10/Jun/17
Let z=x+jy z^2 + 2(1 + j)z + 2 = 0 (x+jy)^2 +2(1+j)(x+jy)+2=0 x^2 −y^2 +2xyj+2(x+xj+yj−y)+2=0 x^2 −y^2 +2xyj+2x+2xj+2yj−2y+2=0 (x^2 −y^2 +2x−2y+2)+( 2xy+2x+2y)j=0+0j x^2 −y^2 +2x−2y+2=0 ∧ 2xy+2x+2y=0 (x−y)(x+y)+2(x−y)+2=0 ∧ x+xy+y=0 (x−y)(x+y+2)+2=0 ∧ y=((−x)/(x+1)) (x−((−x)/(x+1)))(x+((−x)/(x+1))+2)+2=0 ((x^2 +x+x)/(x+1))×((x^2 +x−x+2x+2)/(x+1))+2=0 ((x^2 +2x)/(x+1))×((x^2 +2x+2)/(x+1))+2=0 (x^2 +2x)^2 +2(x^2 +2x)+2(x^2 +2x+1)=0 Let x^2 +2x=t t^2 +2t+2t+2=0 t^2 +4t+2=0 t=((−4±(√(16−8)))/2) t=−2±(√2) x^2 +2x=−2+(√2) ∨ x^2 +2x=−2−(√2) x^2 +2x+2−(√2) =0 ∨ x^2 +2x+2+(√2)=0 x=((−2±(√(4−4(2−(√2)))))/2) ∨ x=((−2±(√(4−4(2+(√2)))))/2) x=((−2±(√(4−8+4(√2)))))/2) ∨ x=((−2±(√(4−8−4(√2)))))/2) x=((−2±(√(−4+4(√2)))))/2) ∨ x=((−2±(√(−4−4(√2)))))/2) x=((−2±2(√((√2)−1)))/2) ∨ x=((−2∓2i(√((√2) +1)))/2) x=−1±(√((√2)−1)) ∨ x=−1∓i(√((√2) +1)) y=((−x)/(x+1)) y=((−(−1±(√((√2)−1)) ))/((−1±(√((√2)−1)) )+1)) ∨ y=((−(−1∓i(√((√2) +1))))/((−1∓i(√((√2) +1)))+1)) y=((1∓(√((√2)−1)) )/(−1±(√((√2)−1)) +1)) ∨ y=((1±i(√((√2) +1)))/(−1∓i(√((√2) +1))+1)) y=((1∓(√((√2)−1)) )/(±(√((√2)−1)) ))×((±(√((√2)−1)) )/(±(√((√2)−1)) )) ∨ y=((1±i(√((√2) +1)))/(∓i(√((√2) +1))))×((∓i(√((√2) +1)))/(∓i(√((√2) +1)))) y=(((1∓(√((√2)−1)) )(±(√((√2)−1)) ))/( (√2)−1 )) ∨ y=(((1±i(√((√2) +1)))(∓i(√((√2) +1))))/(−((√2) +1))) y=((±(√((√2)−1))∓(√2)−1 ))/( (√2)−1 )) ∨ y=((∓i(√((√2) +1))−i^2 (√2) +1))/(−((√2) +1))) y=((±(√((√2)−1))∓(√2)−1 )/( (√2)−1 )) ∨ y=((∓i(√((√2) +1))+(√2) +1)/(−((√2) +1))) Continue
$$\mathrm{Let}\:\mathrm{z}=\mathrm{x}+\mathrm{jy} \\ $$$$\:\mathrm{z}^{\mathrm{2}} \:+\:\mathrm{2}\left(\mathrm{1}\:+\:\mathrm{j}\right)\mathrm{z}\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{jy}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\mathrm{j}\right)\left(\mathrm{x}+\mathrm{jy}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2xyj}+\mathrm{2}\left(\mathrm{x}+\mathrm{xj}+\mathrm{yj}−\mathrm{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2xyj}+\mathrm{2x}+\mathrm{2xj}+\mathrm{2yj}−\mathrm{2y}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2y}+\mathrm{2}\right)+\left(\:\mathrm{2xy}+\mathrm{2x}+\mathrm{2y}\right)\mathrm{j}=\mathrm{0}+\mathrm{0j} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2y}+\mathrm{2}=\mathrm{0}\:\wedge\:\mathrm{2xy}+\mathrm{2x}+\mathrm{2y}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2}\left(\mathrm{x}−\mathrm{y}\right)+\mathrm{2}=\mathrm{0}\:\wedge\:\mathrm{x}+\mathrm{xy}+\mathrm{y}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{2}\right)+\mathrm{2}=\mathrm{0}\:\:\wedge\:\mathrm{y}=\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\left(\mathrm{x}−\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}}\right)\left(\mathrm{x}+\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}}+\mathrm{2}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{x}}{\mathrm{x}+\mathrm{1}}×\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{x}+\mathrm{2x}+\mathrm{2}}{\mathrm{x}+\mathrm{1}}+\mathrm{2}=\mathrm{0} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}}{\mathrm{x}+\mathrm{1}}×\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}{\mathrm{x}+\mathrm{1}}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\right)+\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{Let}\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=\mathrm{t} \\ $$$$\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{2t}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{2}} +\mathrm{4t}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{t}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{8}}}{\mathrm{2}} \\ $$$$\mathrm{t}=−\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=−\mathrm{2}+\sqrt{\mathrm{2}}\:\:\:\vee\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=−\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}−\sqrt{\mathrm{2}}\:=\mathrm{0}\:\:\vee\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}+\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.\mathrm{4}−\mathrm{8}+\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.\mathrm{4}−\mathrm{8}−\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\pm\sqrt{\left.−\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}}\:\:\vee\:\mathrm{x}=\frac{−\mathrm{2}\mp\mathrm{2i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{\mathrm{2}} \\ $$$$\mathrm{x}=−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\:\:\:\vee\:\:\mathrm{x}=−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{−\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{−\left(−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)}{\left(−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\:\:\:\:\:\:\:\mathrm{y}=\frac{−\left(−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)}{\left(−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}{−\mathrm{1}\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\:\:\:\:\:\:\:\mathrm{y}=\frac{\mathrm{1}\pm\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{−\mathrm{1}\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}+\mathrm{1}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}×\frac{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:}\:\:\:\vee\:\:\:\mathrm{y}=\frac{\mathrm{1}\pm\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}×\frac{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}}{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}} \\ $$$$\mathrm{y}=\frac{\left(\mathrm{1}\mp\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)\left(\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\right)}{\:\sqrt{\mathrm{2}}−\mathrm{1}\:}\:\:\vee\:\:\:\mathrm{y}=\frac{\left(\mathrm{1}\pm\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)\left(\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\right)}{−\left(\sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)} \\ $$$$\mathrm{y}=\frac{\left.\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\mp\sqrt{\mathrm{2}}−\mathrm{1}\:\right)}{\:\sqrt{\mathrm{2}}−\mathrm{1}\:}\:\:\vee\:\:\:\mathrm{y}=\frac{\left.\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}−\mathrm{i}^{\mathrm{2}} \sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)}{−\left(\sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)} \\ $$$$\mathrm{y}=\frac{\pm\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\mp\sqrt{\mathrm{2}}−\mathrm{1}\:}{\:\sqrt{\mathrm{2}}−\mathrm{1}\:}\:\:\vee\:\:\:\mathrm{y}=\frac{\mp\mathrm{i}\sqrt{\sqrt{\mathrm{2}}\:\:+\mathrm{1}}+\sqrt{\mathrm{2}}\:\:+\mathrm{1}}{−\left(\sqrt{\mathrm{2}}\:\:+\mathrm{1}\right)} \\ $$$$ \\ $$$$\mathrm{Continue} \\ $$
Commented by tawa tawa last updated on 10/Jun/17
Am with you sir. God bless you sir.
$$\mathrm{Am}\:\mathrm{with}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 09/Jun/17
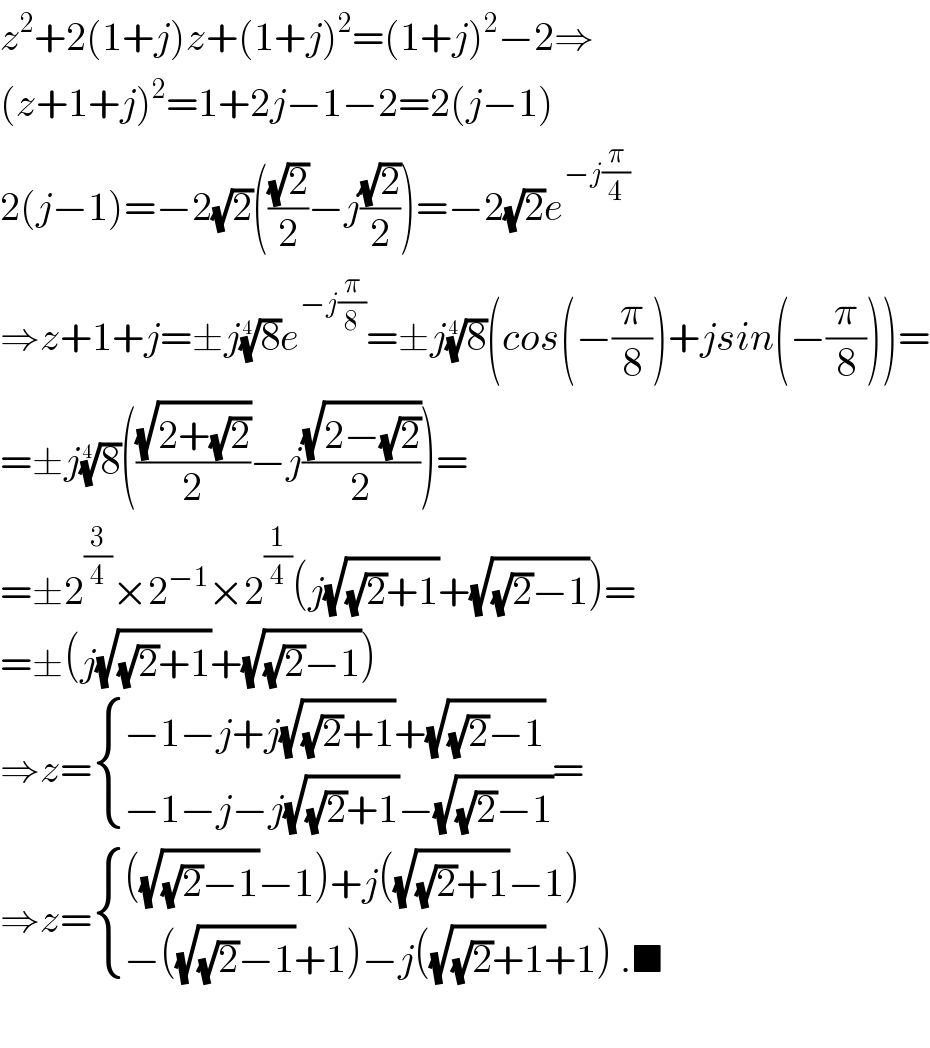
z^2 +2(1+j)z+(1+j)^2 =(1+j)^2 −2⇒ (z+1+j)^2 =1+2j−1−2=2(j−1) 2(j−1)=−2(√2)(((√2)/2)−j((√2)/2))=−2(√2)e^(−j(π/4)) ⇒z+1+j=±j(8)^(1/4) e^(−j(π/8)) =±j(8)^(1/4) (cos(−(π/8))+jsin(−(π/8)))= =±j(8)^(1/4) (((√(2+(√2)))/2)−j((√(2−(√2)))/2))= =±2^(3/4) ×2^(−1) ×2^(1/4) (j(√((√2)+1))+(√((√2)−1)))= =±(j(√((√2)+1))+(√((√2)−1))) ⇒z= { ((−1−j+j(√((√2)+1))+(√((√2)−1)))),((−1−j−j(√((√2)+1))−(√((√2)−1)))) :}= ⇒z= { ((((√((√2)−1))−1)+j((√((√2)+1))−1))),((−((√((√2)−1))+1)−j((√((√2)+1))+1) .■)) :}
$${z}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+{j}\right){z}+\left(\mathrm{1}+{j}\right)^{\mathrm{2}} =\left(\mathrm{1}+{j}\right)^{\mathrm{2}} −\mathrm{2}\Rightarrow \\ $$$$\left({z}+\mathrm{1}+{j}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{j}−\mathrm{1}−\mathrm{2}=\mathrm{2}\left({j}−\mathrm{1}\right) \\ $$$$\mathrm{2}\left({j}−\mathrm{1}\right)=−\mathrm{2}\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{j}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=−\mathrm{2}\sqrt{\mathrm{2}}{e}^{−{j}\frac{\pi}{\mathrm{4}}} \\ $$$$\Rightarrow{z}+\mathrm{1}+{j}=\pm{j}\sqrt[{\mathrm{4}}]{\mathrm{8}}{e}^{−{j}\frac{\pi}{\mathrm{8}}} =\pm{j}\sqrt[{\mathrm{4}}]{\mathrm{8}}\left({cos}\left(−\frac{\pi}{\mathrm{8}}\right)+{jsin}\left(−\frac{\pi}{\mathrm{8}}\right)\right)= \\ $$$$=\pm{j}\sqrt[{\mathrm{4}}]{\mathrm{8}}\left(\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}−{j}\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}}\right)= \\ $$$$=\pm\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} ×\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \left({j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)= \\ $$$$=\pm\left({j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\Rightarrow{z}=\begin{cases}{−\mathrm{1}−{j}+{j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}\\{−\mathrm{1}−{j}−{j}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}\end{cases}= \\ $$$$\Rightarrow{z}=\begin{cases}{\left(\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{1}\right)+{j}\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\mathrm{1}\right)}\\{−\left(\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}+\mathrm{1}\right)−{j}\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}+\mathrm{1}\right)\:.\blacksquare}\end{cases} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 10/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 10/Jun/17
Please sir , am still trying to understand the workings sir. please sir explain to me the steps. i mean the begining
$$\mathrm{Please}\:\mathrm{sir}\:,\:\mathrm{am}\:\mathrm{still}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{workings}\:\mathrm{sir}.\: \\ $$$$\mathrm{please}\:\mathrm{sir}\:\mathrm{explain}\:\mathrm{to}\:\mathrm{me}\:\mathrm{the}\:\mathrm{steps}.\:\mathrm{i}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{begining} \\ $$
Commented by tawa tawa last updated on 11/Jun/17
Sir i am lost from. ± j(2^(3/4) )(cos(−(π/8)) + jsin(−(π/8))] why (−(π/8)) ???. How is it minus sir. i thought it is.... cos((π/8)) − jsin((π/4)) And how is it j(2^(3/4) )(((√(2 + (√2)))/2) − j((√(2 − (√(2 ))))/2)) And the next steps......
$$\mathrm{Sir}\:\mathrm{i}\:\mathrm{am}\:\mathrm{lost}\:\mathrm{from}.\:\pm\:\mathrm{j}\left(\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} \right)\left(\mathrm{cos}\left(−\frac{\pi}{\mathrm{8}}\right)\:+\:\mathrm{jsin}\left(−\frac{\pi}{\mathrm{8}}\right)\right]\: \\ $$$$\mathrm{why}\:\left(−\frac{\pi}{\mathrm{8}}\right)\:???.\:\mathrm{How}\:\mathrm{is}\:\mathrm{it}\:\mathrm{minus}\:\mathrm{sir}.\: \\ $$$$\mathrm{i}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{is}….\:\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}\right)\:−\:\mathrm{jsin}\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{And}\:\mathrm{how}\:\mathrm{is}\:\mathrm{it}\:\:\:\mathrm{j}\left(\mathrm{2}^{\mathrm{3}/\mathrm{4}} \right)\left(\frac{\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}}}}{\mathrm{2}}\:−\:\mathrm{j}\frac{\sqrt{\mathrm{2}\:−\:\sqrt{\mathrm{2}\:}}}{\mathrm{2}}\right) \\ $$$$\mathrm{And}\:\mathrm{the}\:\mathrm{next}\:\mathrm{steps}…… \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17
1)(cosx+jsinx)^n =cosnx+jsinnx 2)e^(jx) =cosx+jsinx 3)e^(−jx) =cos(−x)+jsin(−x)=cosx−jsinx because: cos(−x)=cosx,sin(−x)=−sinx ((√2)/2)−j((√2)/2)=cos(−(π/4))+jsin(−(π/4))=e^(−j(π/4)) angles in cos & sin,should be the same. (z+1+j)^2 =−2(√2)e^(−j(π/4)) =(j)^2 ×2^(3/2) ×e^(−j(π/4)) (√((z+1+j)^2 ))=±(√((j)^2 ×2^(3/2) ×e^(−j(π/4)) )) z+1+j=±j×2^(3/4) ×e^(−j(π/8)) e^(−j(π/8)) =cos(−(π/8))+jsin(−(π/8))=cos((π/8))−jsin((π/8)) cos(π/8)=(√(((1+cos(π/4))/2)=(√((1+((√2)/2))/2))))=((√(2+(√2)))/2)= =(((2)^(1/4) (√((√2)+1)))/2)=2^(1/4) ×2^(−1) ×(√((√2)+1)) sin(π/8)=(√((1−cos(π/4))/2))=(√((1−((√2)/2))/2))=((√(2−(√2)))/2)= =(((2)^(1/4) (√((√2)−1)))/2)=2^(1/4) ×2^(−1) ×(√((√2)−1)) ⇒z+1+j=±j×2^(3/4) ×2^(1/4) ×2^(−1) ((√((√2)+1))−j(√((√2)−1)))= =±j×2^((3/4)+(1/4)−1) ((√((√2)+1))−j(√((√2)−1)))= =±j×1×((√((√2)+1))−j(√((√2)−1)))=±j(.....) is it ok? miss tawa?
$$\left.\mathrm{1}\right)\left({cosx}+{jsinx}\right)^{{n}} ={cosnx}+{jsinnx} \\ $$$$\left.\mathrm{2}\right){e}^{{jx}} ={cosx}+{jsinx} \\ $$$$\left.\mathrm{3}\right){e}^{−{jx}} ={cos}\left(−{x}\right)+{jsin}\left(−{x}\right)={cosx}−{jsinx} \\ $$$${because}:\:{cos}\left(−{x}\right)={cosx},{sin}\left(−{x}\right)=−{sinx} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{j}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}={cos}\left(−\frac{\pi}{\mathrm{4}}\right)+{jsin}\left(−\frac{\pi}{\mathrm{4}}\right)={e}^{−{j}\frac{\pi}{\mathrm{4}}} \\ $$$${angles}\:{in}\:{cos}\:\&\:{sin},{should}\:{be}\:{the}\:{same}. \\ $$$$\left({z}+\mathrm{1}+{j}\right)^{\mathrm{2}} =−\mathrm{2}\sqrt{\mathrm{2}}{e}^{−{j}\frac{\pi}{\mathrm{4}}} =\left({j}\right)^{\mathrm{2}} ×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} ×{e}^{−{j}\frac{\pi}{\mathrm{4}}} \\ $$$$\sqrt{\left({z}+\mathrm{1}+{j}\right)^{\mathrm{2}} }=\pm\sqrt{\left({j}\right)^{\mathrm{2}} ×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} ×{e}^{−{j}\frac{\pi}{\mathrm{4}}} } \\ $$$${z}+\mathrm{1}+{j}=\pm{j}×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} ×{e}^{−{j}\frac{\pi}{\mathrm{8}}} \\ $$$${e}^{−{j}\frac{\pi}{\mathrm{8}}} ={cos}\left(−\frac{\pi}{\mathrm{8}}\right)+{jsin}\left(−\frac{\pi}{\mathrm{8}}\right)={cos}\left(\frac{\pi}{\mathrm{8}}\right)−{jsin}\left(\frac{\pi}{\mathrm{8}}\right) \\ $$$${cos}\frac{\pi}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}+{cos}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}}}=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}= \\ $$$$=\frac{\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}}{\mathrm{2}}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} ×\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$${sin}\frac{\pi}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}−{cos}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{2}}= \\ $$$$=\frac{\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} ×\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\Rightarrow{z}+\mathrm{1}+{j}=\pm{j}×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}} ×\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\mathrm{2}^{−\mathrm{1}} \left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−{j}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)= \\ $$$$=\pm\boldsymbol{{j}}×\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\boldsymbol{{j}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)= \\ $$$$=\pm\boldsymbol{{j}}×\mathrm{1}×\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}−\boldsymbol{{j}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)=\pm\boldsymbol{{j}}\left(…..\right)\: \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{it}}\:\boldsymbol{{ok}}?\:\boldsymbol{{miss}}\:\boldsymbol{{tawa}}? \\ $$
Commented by tawa tawa last updated on 11/Jun/17
Yes sir. i understand very well now. God bless you sir. i really appreciate your time sir.
$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well}\:\mathrm{now}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate} \\ $$$$\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *