Question Number 20619 by Tinkutara last updated on 29/Aug/17
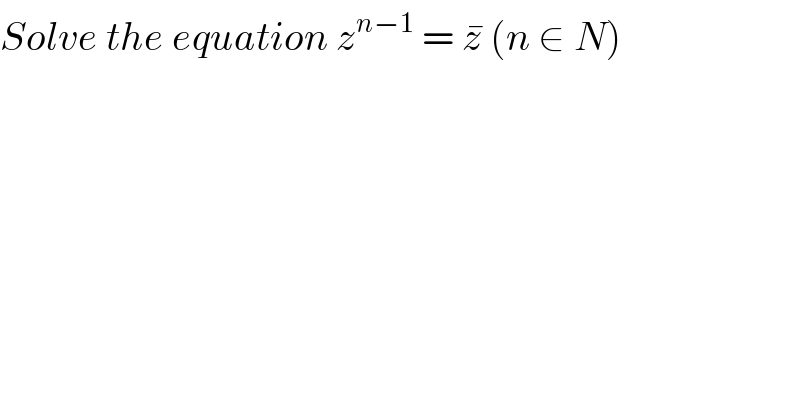
$${Solve}\:{the}\:{equation}\:{z}^{{n}−\mathrm{1}} \:=\:\bar {{z}}\:\left({n}\:\in\:{N}\right) \\ $$
Answered by ajfour last updated on 29/Aug/17
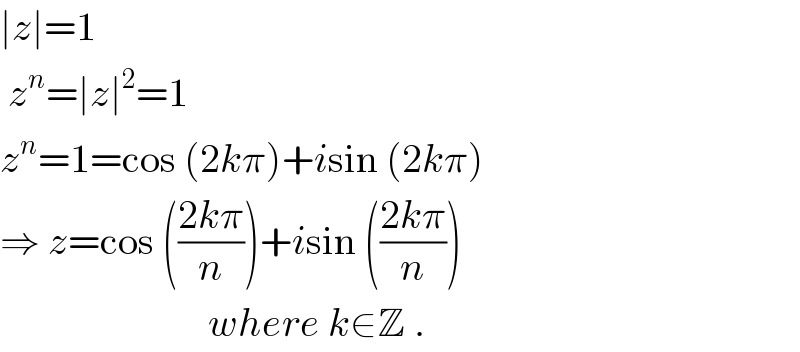
$$\mid{z}\mid=\mathrm{1}\: \\ $$$$\:{z}^{{n}} =\mid{z}\mid^{\mathrm{2}} =\mathrm{1} \\ $$$${z}^{{n}} =\mathrm{1}=\mathrm{cos}\:\left(\mathrm{2}{k}\pi\right)+{i}\mathrm{sin}\:\left(\mathrm{2}{k}\pi\right) \\ $$$$\Rightarrow\:{z}=\mathrm{cos}\:\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)+{i}\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{{n}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{where}\:{k}\in\mathbb{Z}\:. \\ $$
Commented by Tinkutara last updated on 29/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
