solve-the-eqution-2-x-12-4x-1-2-x-x-2-

Question Number 100916 by 175 last updated on 29/Jun/20

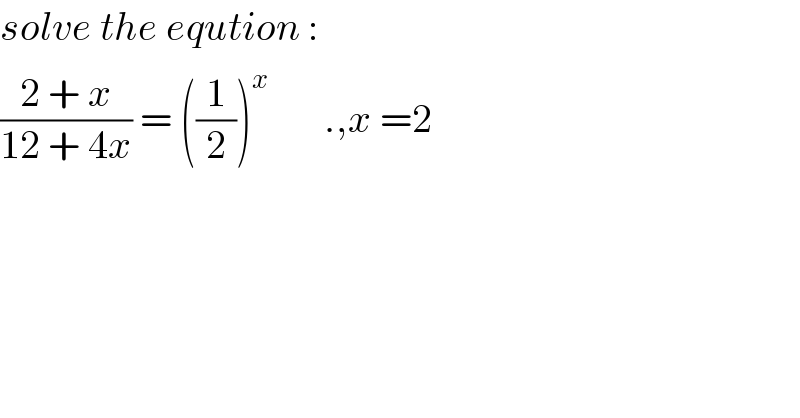
s o l v e t h e e q u t i o n :

\frac{2 + x}{12 + 4 x} = {(\frac{1}{2})}^{x} ., x = 2

Answered by 1549442205 last updated on 30/Jun/20

\Leftrightarrow 2^{x} - \frac{12 + 4 x}{2 + x} = 0 \Leftrightarrow 2^{x} - \frac{6}{x + 2} - 4 = 0 (*)

\Rightarrow x = 2.421432378

putting f (x) = 2^{x} - \frac{6}{x + 2} - 4 \Rightarrow f^{'} (x) =

2^{x} \ln 2 + \frac{6}{{(x + 2)}^{2}} > 0 \forall x \in (- \infty; + \infty) . so

f (x) is increasing function on (- \infty; + \infty)

Hence, x = 2.421432378 is unique root

of the equation (*)