Question Number 89243 by M±th+et£s last updated on 16/Apr/20
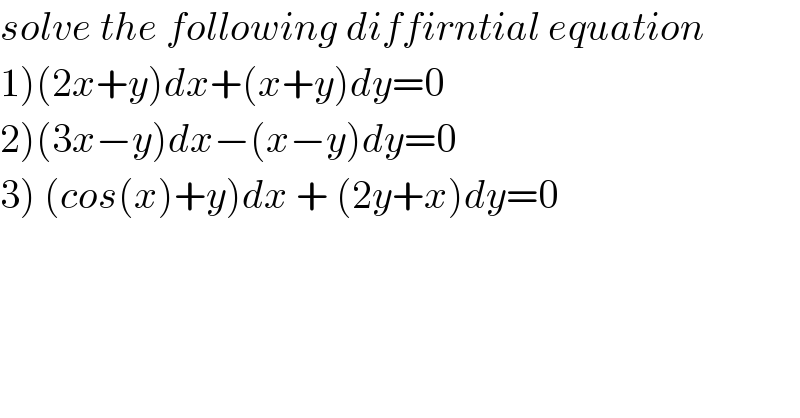
$${solve}\:{the}\:{following}\:{diffirntial}\:{equation} \\ $$$$\left.\mathrm{1}\right)\left(\mathrm{2}{x}+{y}\right){dx}+\left({x}+{y}\right){dy}=\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\left(\mathrm{3}{x}−{y}\right){dx}−\left({x}−{y}\right){dy}=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\:\left({cos}\left({x}\right)+{y}\right){dx}\:+\:\left(\mathrm{2}{y}+{x}\right){dy}=\mathrm{0} \\ $$
Answered by TANMAY PANACEA. last updated on 16/Apr/20
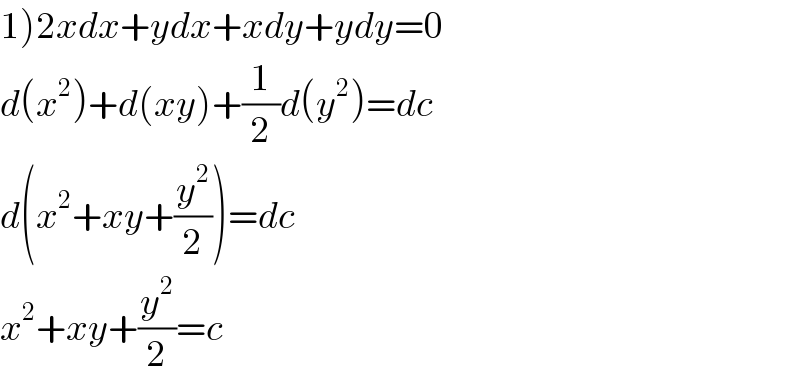
$$\left.\mathrm{1}\right)\mathrm{2}{xdx}+{ydx}+{xdy}+{ydy}=\mathrm{0} \\ $$$${d}\left({x}^{\mathrm{2}} \right)+{d}\left({xy}\right)+\frac{\mathrm{1}}{\mathrm{2}}{d}\left({y}^{\mathrm{2}} \right)={dc} \\ $$$${d}\left({x}^{\mathrm{2}} +{xy}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\right)={dc} \\ $$$${x}^{\mathrm{2}} +{xy}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}={c} \\ $$
Answered by TANMAY PANACEA. last updated on 16/Apr/20
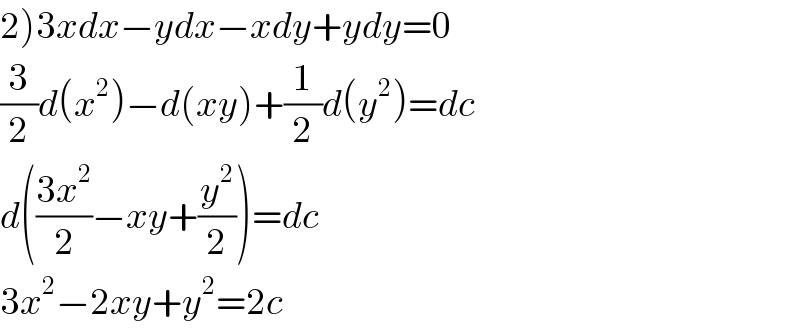
$$\left.\mathrm{2}\right)\mathrm{3}{xdx}−{ydx}−{xdy}+{ydy}=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{d}\left({x}^{\mathrm{2}} \right)−{d}\left({xy}\right)+\frac{\mathrm{1}}{\mathrm{2}}{d}\left({y}^{\mathrm{2}} \right)={dc} \\ $$$${d}\left(\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}−{xy}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\right)={dc} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} =\mathrm{2}{c} \\ $$
Answered by TANMAY PANACEA. last updated on 16/Apr/20
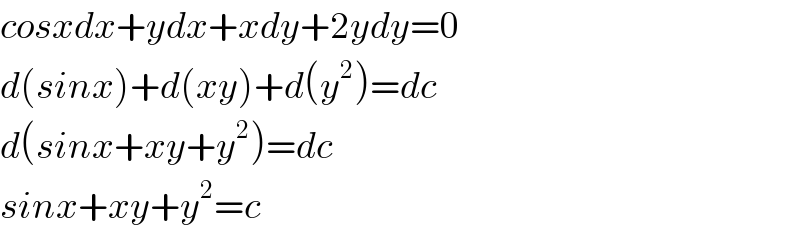
$${cosxdx}+{ydx}+{xdy}+\mathrm{2}{ydy}=\mathrm{0} \\ $$$${d}\left({sinx}\right)+{d}\left({xy}\right)+{d}\left({y}^{\mathrm{2}} \right)={dc} \\ $$$${d}\left({sinx}+{xy}+{y}^{\mathrm{2}} \right)={dc} \\ $$$${sinx}+{xy}+{y}^{\mathrm{2}} ={c} \\ $$
Commented by M±th+et£s last updated on 16/Apr/20
$${hod}\:{bless}\:{you}\:{sir}\:. \\ $$
