Question Number 86307 by niroj last updated on 28/Mar/20
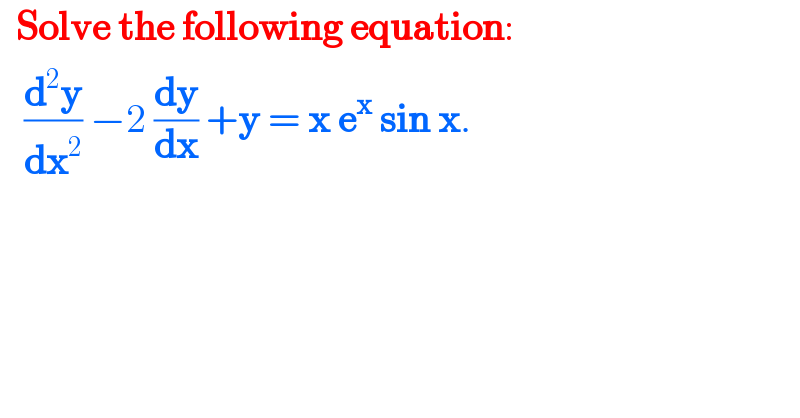
$$\:\:\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{following}}\:\boldsymbol{\mathrm{equation}}: \\ $$$$\:\:\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }\:−\mathrm{2}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\:+\boldsymbol{\mathrm{y}}\:=\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}. \\ $$
Answered by TANMAY PANACEA. last updated on 28/Mar/20
![y=e^(mx) (m^2 −2m+1)e^(mx) =0 e^(mx) ≠0 m=1,1 C.F=Ae^x +Bxe^x P.I=((xe^x sinx)/(D^2 −2D+1)) =e^x .((xsinx)/((D+1)^2 −2(D+1)+1)) =e^x .((xsinx)/(D^2 +2D+1−2D−2+1)) =e^x .((xsinx)/D^2 ) now ((f(x))/D)=∫f(x)dx ∫xsinxdx x∫sinxdx−∫[(dx/dx)∫sinxdx]dx −xcosx+∫cosxdx =−xcosx+sinx+c ∫(−xcosx+sinx+c ) dx→((xsinx)/D^2 ) −x∫cosxdx+∫[(dx/dx)∫cosxdx]dx−cosx+cx+c_1 −xsinx−sinx−cosx+cx+c_1 y=Ae^x +Bxe^x −(1+x)sinx−cosx+cx+c_1](https://www.tinkutara.com/question/Q86325.png)
$${y}={e}^{{mx}} \\ $$$$\left({m}^{\mathrm{2}} −\mathrm{2}{m}+\mathrm{1}\right){e}^{{mx}} =\mathrm{0} \\ $$$${e}^{{mx}} \neq\mathrm{0}\:\:{m}=\mathrm{1},\mathrm{1} \\ $$$${C}.{F}={Ae}^{{x}} +{Bxe}^{{x}} \\ $$$${P}.{I}=\frac{{xe}^{{x}} {sinx}}{{D}^{\mathrm{2}} −\mathrm{2}{D}+\mathrm{1}} \\ $$$$={e}^{{x}} .\frac{{xsinx}}{\left({D}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({D}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$={e}^{{x}} .\frac{{xsinx}}{{D}^{\mathrm{2}} +\mathrm{2}{D}+\mathrm{1}−\mathrm{2}{D}−\mathrm{2}+\mathrm{1}} \\ $$$$={e}^{{x}} .\frac{{xsinx}}{{D}^{\mathrm{2}} } \\ $$$${now}\:\frac{{f}\left({x}\right)}{{D}}=\int{f}\left({x}\right){dx} \\ $$$$\int{xsinxdx} \\ $$$${x}\int{sinxdx}−\int\left[\frac{{dx}}{{dx}}\int{sinxdx}\right]{dx} \\ $$$$−{xcosx}+\int{cosxdx} \\ $$$$=−{xcosx}+{sinx}+{c} \\ $$$$\int\left(−{xcosx}+{sinx}+{c}\:\right)\:{dx}\rightarrow\frac{{xsinx}}{{D}^{\mathrm{2}} } \\ $$$$−{x}\int{cosxdx}+\int\left[\frac{{dx}}{{dx}}\int{cosxdx}\right]{dx}−{cosx}+{cx}+{c}_{\mathrm{1}} \\ $$$$−{xsinx}−{sinx}−{cosx}+{cx}+{c}_{\mathrm{1}} \\ $$$${y}={Ae}^{{x}} +{Bxe}^{{x}} −\left(\mathrm{1}+{x}\right){sinx}−{cosx}+{cx}+{c}_{\mathrm{1}} \\ $$
Commented by niroj last updated on 28/Mar/20
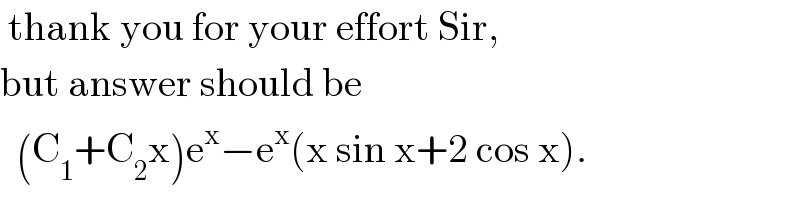
$$\:\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{Sir}, \\ $$$$\mathrm{but}\:\mathrm{answer}\:\mathrm{should}\:\mathrm{be}\: \\ $$$$\:\:\left(\mathrm{C}_{\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \mathrm{x}\right)\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{2}\:\mathrm{cos}\:\mathrm{x}\right). \\ $$
Commented by TANMAY PANACEA. last updated on 28/Mar/20

$${let}\:{me}\:{check} \\ $$
