Menu Close

solve-the-following-initial-values-DEs-20y-4y-y-0-y-0-3-2-and-y-0-0-

Tinku Tara 0 Comments
Pin




Question Number 98255 by john santu last updated on 12/Jun/20
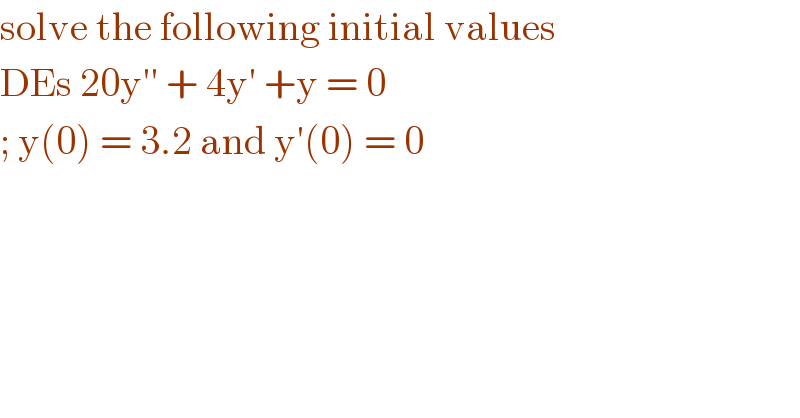
solve the following initial values DEs 20y′′ + 4y′ +y = 0 ; y(0) = 3.2 and y′(0) = 0
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{following}\:\mathrm{initial}\:\mathrm{values} \\ $$$$\mathrm{DEs}\:\mathrm{20y}''\:+\:\mathrm{4y}'\:+\mathrm{y}\:=\:\mathrm{0} \\ $$$$;\:\mathrm{y}\left(\mathrm{0}\right)\:=\:\mathrm{3}.\mathrm{2}\:\mathrm{and}\:\mathrm{y}'\left(\mathrm{0}\right)\:=\:\mathrm{0}\: \\ $$
Commented by bemath last updated on 13/Jun/20
auxilary equation euler−cauchy 20m^2 +4m+1=0 m=−(1/(10))± (i/5) ∴y=e^(−(x/(10))) [Acos (x/5)+Bsin (x/5)] ⇒y(0)=3.2⇒A=3.2 y′(x)= e^(−(x/(10))) (−((3.2)/5)sin (x/5)+(B/5)sin (x/5)) y′(0)=0 ⇒B=((3.2)/2) = 1.6 hence y(x)= e^(−(x/(10))) (3.2 cos (x/5) + 1.6 sin (x/5)) ■
$$\mathrm{auxilary}\:\mathrm{equation}\:\mathrm{euler}−\mathrm{cauchy} \\ $$$$\mathrm{20m}^{\mathrm{2}} +\mathrm{4m}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{m}=−\frac{\mathrm{1}}{\mathrm{10}}\pm\:\frac{{i}}{\mathrm{5}}\:\therefore\mathrm{y}=\mathrm{e}^{−\frac{{x}}{\mathrm{10}}} \:\left[{A}\mathrm{cos}\:\frac{{x}}{\mathrm{5}}+{B}\mathrm{sin}\:\frac{{x}}{\mathrm{5}}\right] \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{0}\right)=\mathrm{3}.\mathrm{2}\Rightarrow\mathrm{A}=\mathrm{3}.\mathrm{2} \\ $$$$\mathrm{y}'\left(\mathrm{x}\right)=\:\mathrm{e}^{−\frac{{x}}{\mathrm{10}}} \:\left(−\frac{\mathrm{3}.\mathrm{2}}{\mathrm{5}}\mathrm{sin}\:\frac{{x}}{\mathrm{5}}+\frac{{B}}{\mathrm{5}}\mathrm{sin}\:\frac{{x}}{\mathrm{5}}\right) \\ $$$$\mathrm{y}'\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\mathrm{B}=\frac{\mathrm{3}.\mathrm{2}}{\mathrm{2}}\:=\:\mathrm{1}.\mathrm{6} \\ $$$$\mathrm{hence}\:\mathrm{y}\left(\mathrm{x}\right)=\:\mathrm{e}^{−\frac{{x}}{\mathrm{10}}} \:\left(\mathrm{3}.\mathrm{2}\:\mathrm{cos}\:\frac{{x}}{\mathrm{5}}\:+\:\mathrm{1}.\mathrm{6}\:\mathrm{sin}\:\frac{{x}}{\mathrm{5}}\right)\:\blacksquare \\ $$
Answered by Mr.D.N. last updated on 12/Jun/20
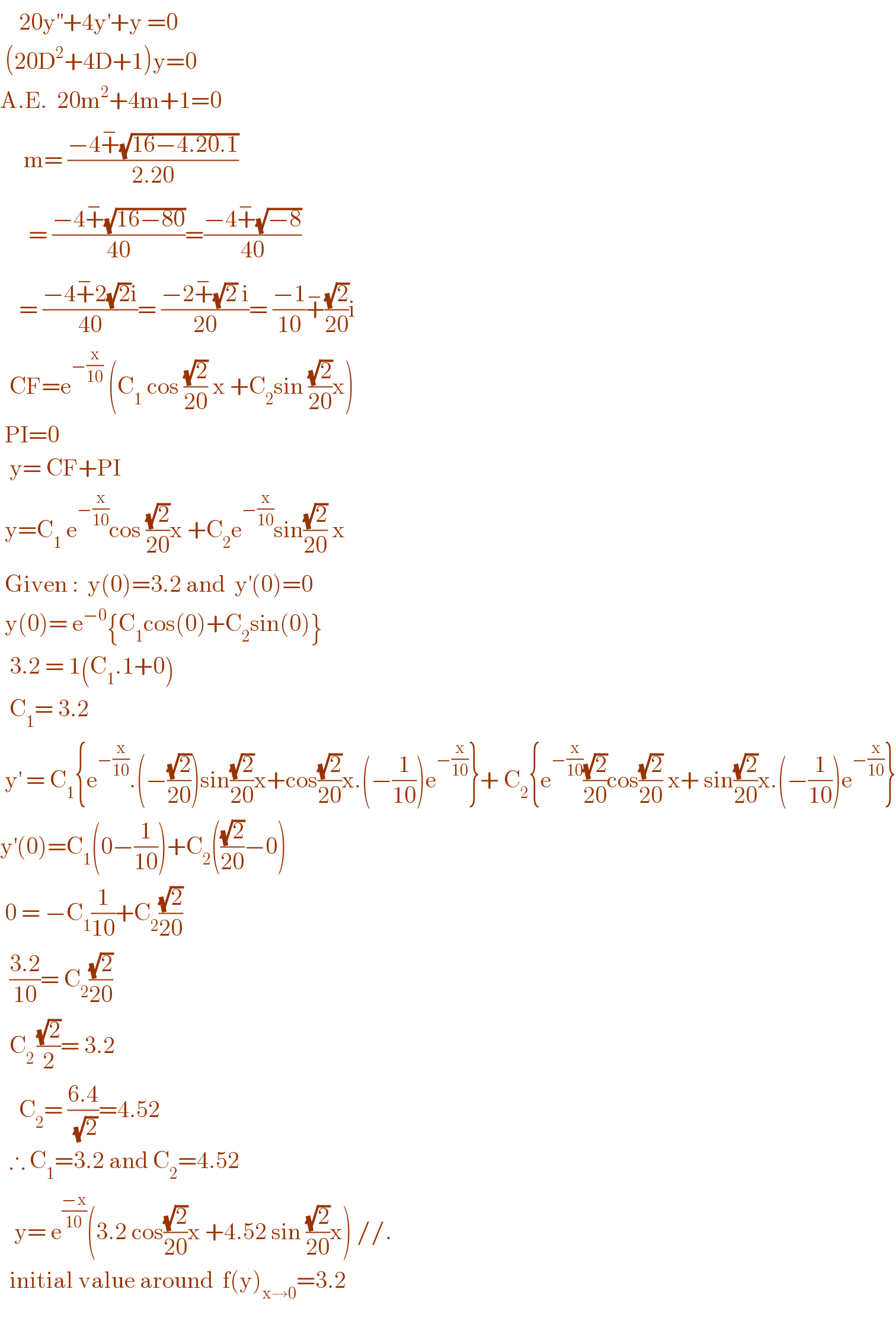
20y^(′′) +4y^′ +y =0 (20D^2 +4D+1)y=0 A.E. 20m^2 +4m+1=0 m= ((−4+^− (√(16−4.20.1)))/(2.20)) = ((−4+^− (√(16−80)))/(40))=((−4+^− (√(−8)))/(40)) = ((−4+^− 2(√2)i)/(40))= ((−2+^− (√2) i)/(20))= ((−1)/(10))+^− ((√2)/(20))i CF=e^(−(x/(10))) (C_1 cos ((√2)/(20)) x +C_2 sin ((√2)/(20))x) PI=0 y= CF+PI y=C_1 e^(−(x/(10))) cos ((√2)/(20))x +C_2 e^(−(x/(10))) sin((√2)/(20)) x Given : y(0)=3.2 and y^′ (0)=0 y(0)= e^(−0) {C_1 cos(0)+C_2 sin(0)} 3.2 = 1(C_1 .1+0) C_1 = 3.2 y^′ = C_1 {e^(−(x/(10))) .(−((√2)/(20)))sin((√2)/(20))x+cos((√2)/(20))x.(−(1/(10)))e^(−(x/(10))) }+ C_2 {e^(−(x/(10))) ((√2)/(20))cos((√2)/(20)) x+ sin((√2)/(20))x.(−(1/(10)))e^(−(x/(10))) } y^′ (0)=C_1 (0−(1/(10)))+C_2 (((√2)/(20))−0) 0 = −C_1 (1/(10))+C_2 ((√2)/(20)) ((3.2)/(10))= C_2 ((√2)/(20)) C_(2 ) ((√2)/2)= 3.2 C_2 = ((6.4)/( (√2)))=4.52 ∴ C_1 =3.2 and C_2 =4.52 y= e^((−x)/(10)) (3.2 cos((√2)/(20))x +4.52 sin ((√2)/(20))x) //. initial value around f(y)_(x→0) =3.2
$$\:\:\:\:\mathrm{20y}^{''} +\mathrm{4y}^{'} +\mathrm{y}\:=\mathrm{0} \\ $$$$\:\left(\mathrm{20D}^{\mathrm{2}} +\mathrm{4D}+\mathrm{1}\right)\mathrm{y}=\mathrm{0} \\ $$$$\mathrm{A}.\mathrm{E}.\:\:\mathrm{20m}^{\mathrm{2}} +\mathrm{4m}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{m}=\:\frac{−\mathrm{4}\overset{−} {+}\sqrt{\mathrm{16}−\mathrm{4}.\mathrm{20}.\mathrm{1}}}{\mathrm{2}.\mathrm{20}} \\ $$$$\:\:\:\:\:\:=\:\frac{−\mathrm{4}\overset{−} {+}\sqrt{\mathrm{16}−\mathrm{80}}}{\mathrm{40}}=\frac{−\mathrm{4}\overset{−} {+}\sqrt{−\mathrm{8}}}{\mathrm{40}} \\ $$$$\:\:\:\:=\:\frac{−\mathrm{4}\overset{−} {+}\mathrm{2}\sqrt{\mathrm{2}}\mathrm{i}}{\mathrm{40}}=\:\frac{−\mathrm{2}\overset{−} {+}\sqrt{\mathrm{2}}\:\mathrm{i}}{\mathrm{20}}=\:\frac{−\mathrm{1}}{\mathrm{10}}\overset{−} {+}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{i} \\ $$$$\:\:\mathrm{CF}=\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} \:\left(\mathrm{C}_{\mathrm{1}} \:\mathrm{cos}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\:\mathrm{x}\:+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}\right) \\ $$$$\:\mathrm{PI}=\mathrm{0} \\ $$$$\:\:\mathrm{y}=\:\mathrm{CF}+\mathrm{PI} \\ $$$$\:\mathrm{y}=\mathrm{C}_{\mathrm{1}} \:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} \mathrm{cos}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}\:+\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} \mathrm{sin}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\:\mathrm{x} \\ $$$$\:\mathrm{Given}\::\:\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{3}.\mathrm{2}\:\mathrm{and}\:\:\mathrm{y}^{'} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\mathrm{y}\left(\mathrm{0}\right)=\:\mathrm{e}^{−\mathrm{0}} \left\{\mathrm{C}_{\mathrm{1}} \mathrm{cos}\left(\mathrm{0}\right)+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\left(\mathrm{0}\right)\right\} \\ $$$$\:\:\mathrm{3}.\mathrm{2}\:=\:\mathrm{1}\left(\mathrm{C}_{\mathrm{1}} .\mathrm{1}+\mathrm{0}\right) \\ $$$$\:\:\mathrm{C}_{\mathrm{1}} =\:\mathrm{3}.\mathrm{2} \\ $$$$\:\mathrm{y}^{'} \:=\:\mathrm{C}_{\mathrm{1}} \left\{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} .\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\right)\mathrm{sin}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}+\mathrm{cos}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}.\left(−\frac{\mathrm{1}}{\mathrm{10}}\right)\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} \right\}+\:\mathrm{C}_{\mathrm{2}} \left\{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} \frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{cos}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\:\mathrm{x}+\:\mathrm{sin}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}.\left(−\frac{\mathrm{1}}{\mathrm{10}}\right)\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{10}}} \right\} \\ $$$$\mathrm{y}^{'} \left(\mathrm{0}\right)=\mathrm{C}_{\mathrm{1}} \left(\mathrm{0}−\frac{\mathrm{1}}{\mathrm{10}}\right)+\mathrm{C}_{\mathrm{2}} \left(\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}−\mathrm{0}\right) \\ $$$$\:\mathrm{0}\:=\:−\mathrm{C}_{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{10}}+\mathrm{C}_{\mathrm{2}} \frac{\sqrt{\mathrm{2}}}{\mathrm{20}} \\ $$$$\:\:\frac{\mathrm{3}.\mathrm{2}}{\mathrm{10}}=\:\mathrm{C}_{\mathrm{2}} \frac{\sqrt{\mathrm{2}}}{\mathrm{20}} \\ $$$$\:\:\mathrm{C}_{\mathrm{2}\:} \frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\:\mathrm{3}.\mathrm{2} \\ $$$$\:\:\:\:\mathrm{C}_{\mathrm{2}} =\:\frac{\mathrm{6}.\mathrm{4}}{\:\sqrt{\mathrm{2}}}=\mathrm{4}.\mathrm{52} \\ $$$$\:\:\therefore\:\mathrm{C}_{\mathrm{1}} =\mathrm{3}.\mathrm{2}\:\mathrm{and}\:\mathrm{C}_{\mathrm{2}} =\mathrm{4}.\mathrm{52} \\ $$$$\:\:\:\mathrm{y}=\:\mathrm{e}^{\frac{−\mathrm{x}}{\mathrm{10}}} \left(\mathrm{3}.\mathrm{2}\:\mathrm{cos}\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}\:+\mathrm{4}.\mathrm{52}\:\mathrm{sin}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{x}\right)\://. \\ $$$$\:\:\mathrm{initial}\:\mathrm{value}\:\mathrm{around}\:\:\mathrm{f}\left(\mathrm{y}\right)_{\mathrm{x}\rightarrow\mathrm{0}} =\mathrm{3}.\mathrm{2} \\ $$$$\: \\ $$
Commented by bemath last updated on 13/Jun/20
wrong in (√(16−80)) = (√(−8))
$$\mathrm{wrong}\:\mathrm{in}\:\sqrt{\mathrm{16}−\mathrm{80}}\:=\:\sqrt{−\mathrm{8}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *