Question Number 105704 by 1549442205PVT last updated on 31/Jul/20
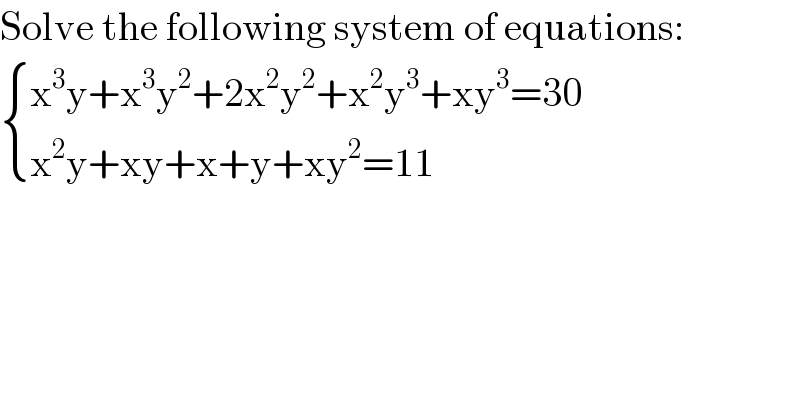
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{following}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{3}} \mathrm{y}+\mathrm{x}^{\mathrm{3}} \mathrm{y}^{\mathrm{2}} +\mathrm{2x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{3}} +\mathrm{xy}^{\mathrm{3}} =\mathrm{30}}\\{\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xy}+\mathrm{x}+\mathrm{y}+\mathrm{xy}^{\mathrm{2}} =\mathrm{11}}\end{cases} \\ $$
Commented by PRITHWISH SEN 2 last updated on 31/Jul/20

$$\mathrm{from}\:\mathrm{eqn}.\:\left(\mathrm{i}\right) \\ $$$$\mathrm{xy}\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{xy}\right)=\mathrm{30}………\left(\mathrm{iii}\right) \\ $$$$\mathrm{from}\:\mathrm{eqn}.\:\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{xy}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{1}\right)=\mathrm{12}…..\left(\mathrm{iv}\right) \\ $$$$\boldsymbol{\mathrm{now}}\:\boldsymbol{\mathrm{put}}\:\:\:\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{a}}\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{xy}}=\boldsymbol{\mathrm{b}} \\ $$$$\boldsymbol{\mathrm{then}}\:\left(\boldsymbol{\mathrm{iii}}\right)\Rightarrow\:\mathrm{ab}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{30} \\ $$$$\left(\mathrm{iv}\right)\Rightarrow\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{b}+\mathrm{1}\right)=\mathrm{12}\Rightarrow\:\mathrm{ab}+\mathrm{a}+\mathrm{b}=\mathrm{11} \\ $$$$\boldsymbol{\mathrm{solving}}\:\:\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{ab}}\right)=\left(\mathrm{5},\mathrm{6}\right)\:\mathrm{or}\:\left(\mathrm{6},\mathrm{5}\right) \\ $$$$\therefore\:\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\right)=\left(\mathrm{5},\mathrm{1}\right),\left(\mathrm{1},\mathrm{5}\right),\left(\mathrm{3},\mathrm{2}\right)\:\boldsymbol{\mathrm{or}}\:\left(\mathrm{2},\mathrm{3}\right) \\ $$$$\mathrm{for}\:\left(\mathrm{5},\mathrm{1}\right) \\ $$$$\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)=\:\left\{\left(\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} ,\left(\frac{\sqrt{\mathrm{7}}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \right\}\:\mathrm{and}\:\left\{\left(\frac{\sqrt{\mathrm{7}}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} ,\left(\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \right\} \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{real}\:\mathrm{value}\:\mathrm{for}\:\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{1},\mathrm{5}\right) \\ $$$$\mathrm{for}\:\left(\mathrm{3},\mathrm{2}\right) \\ $$$$\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)=\:\left(\mathrm{2},\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{1},\mathrm{2}\right) \\ $$$$\mathrm{and}\:\mathrm{no}\:\mathrm{real}\:\mathrm{value}\:\mathrm{for}\:\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{2},\mathrm{3}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 31/Jul/20

$$\mathrm{welcome} \\ $$
Answered by 1549442205PVT last updated on 31/Jul/20
![Set x+y=u,xy=v we have (1)⇔xy(x^2 +y^2 )+(xy)^2 (x+y)+2(xy)^2 =30 ⇔xy[(x+y)^2 −2xy]+(xy)^2 (x+y)+2(xy)^2 =30 (x+y)^2 (xy)+(xy)^2 (x+y)=30 (2)⇔xy(x+y)+xy+x+y=11. { ((u^2 v+v^2 u=30)),((uv+i+v=11)) :}⇔ { ((uv(u+v)=30)),((uv+u+v=11)) :} Set u+v=m,uv=n⇒ { ((m+n=11)),((mn=30)) :} ⇔(m,n)∈{(5,6),(6,5)} i)(m,n)=(5,6)⇔(u,v)∈{(3,2),(2,3)} +(u,v)=(3,2)⇔ { ((x+y=3)),((xy=2)) :}⇔(x,y)∈{(2,1),(1,2)} +(u,v)=(2,3)⇔ { ((x+y=2)),((xy=3)) :}⇒(x−y)^2 =(x+y)^2 −4xy=−8<0 This case has no roots ii)(m,n)=(6,5)⇔(u,v)∈{(5,1),(1,5)} +(u,v)=(5,1)⇔ { ((x+y=5)),((xy=1)) :}⇔ { ((x+y=5)),(((x−y)^2 =(x+y)^2 −4xy=21)) :} ⇔ { ((x+y=5)),((x−y=±(√(21)))) :} ⇔(x,y)∈{(((5+(√(21)))/2),((5−(√(21)))/2)),(((5−(√(21)))/2),((5+(√(21)))/2))} +(u,v)=(1,5)⇔ { ((x+y=1)),((xy=5)) :}⇒(x−y)^2 =(x+y)^2 −4xy=−19<0 so this case has no roots Thus,the given system has four roots: (x,y)∈{(1,2),(2,1),(((5+(√(21)))/2),((5−(√(21)))/2)),(((5−(√(21)))/2),((5+(√(21)))/2))](https://www.tinkutara.com/question/Q105737.png)
$$\mathrm{Set}\:\mathrm{x}+\mathrm{y}=\mathrm{u},\mathrm{xy}=\mathrm{v}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{xy}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)+\left(\mathrm{xy}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2}\left(\mathrm{xy}\right)^{\mathrm{2}} =\mathrm{30} \\ $$$$\Leftrightarrow\mathrm{xy}\left[\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2xy}\right]+\left(\mathrm{xy}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{y}\right)+\mathrm{2}\left(\mathrm{xy}\right)^{\mathrm{2}} =\mathrm{30} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} \left(\mathrm{xy}\right)+\left(\mathrm{xy}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{y}\right)=\mathrm{30} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\mathrm{xy}\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{xy}+\mathrm{x}+\mathrm{y}=\mathrm{11}. \\ $$$$\begin{cases}{\mathrm{u}^{\mathrm{2}} \mathrm{v}+\mathrm{v}^{\mathrm{2}} \mathrm{u}=\mathrm{30}}\\{\mathrm{uv}+\mathrm{i}+\mathrm{v}=\mathrm{11}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{uv}\left(\mathrm{u}+\mathrm{v}\right)=\mathrm{30}}\\{\mathrm{uv}+\mathrm{u}+\mathrm{v}=\mathrm{11}}\end{cases} \\ $$$$\mathrm{Set}\:\mathrm{u}+\mathrm{v}=\mathrm{m},\mathrm{uv}=\mathrm{n}\Rightarrow\begin{cases}{\mathrm{m}+\mathrm{n}=\mathrm{11}}\\{\mathrm{mn}=\mathrm{30}}\end{cases} \\ $$$$\Leftrightarrow\left(\mathrm{m},\mathrm{n}\right)\in\left\{\left(\mathrm{5},\mathrm{6}\right),\left(\mathrm{6},\mathrm{5}\right)\right\} \\ $$$$\left.\mathrm{i}\right)\left(\mathrm{m},\mathrm{n}\right)=\left(\mathrm{5},\mathrm{6}\right)\Leftrightarrow\left(\mathrm{u},\mathrm{v}\right)\in\left\{\left(\mathrm{3},\mathrm{2}\right),\left(\mathrm{2},\mathrm{3}\right)\right\} \\ $$$$+\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{3},\mathrm{2}\right)\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{3}}\\{\mathrm{xy}=\mathrm{2}}\end{cases}\Leftrightarrow\left(\mathrm{x},\mathrm{y}\right)\in\left\{\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{1},\mathrm{2}\right)\right\} \\ $$$$+\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{2},\mathrm{3}\right)\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{2}}\\{\mathrm{xy}=\mathrm{3}}\end{cases}\Rightarrow\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{4xy}=−\mathrm{8}<\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{case}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\left.\mathrm{ii}\right)\left(\mathrm{m},\mathrm{n}\right)=\left(\mathrm{6},\mathrm{5}\right)\Leftrightarrow\left(\mathrm{u},\mathrm{v}\right)\in\left\{\left(\mathrm{5},\mathrm{1}\right),\left(\mathrm{1},\mathrm{5}\right)\right\} \\ $$$$+\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{5},\mathrm{1}\right)\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{5}}\\{\mathrm{xy}=\mathrm{1}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{5}}\\{\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{4xy}=\mathrm{21}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{5}}\\{\mathrm{x}−\mathrm{y}=\pm\sqrt{\mathrm{21}}}\end{cases}\:\Leftrightarrow\left(\mathrm{x},\mathrm{y}\right)\in\left\{\left(\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}},\frac{\mathrm{5}−\sqrt{\mathrm{21}}}{\mathrm{2}}\right),\left(\frac{\mathrm{5}−\sqrt{\mathrm{21}}}{\mathrm{2}},\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}}\right)\right\} \\ $$$$+\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{1},\mathrm{5}\right)\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{1}}\\{\mathrm{xy}=\mathrm{5}}\end{cases}\Rightarrow\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{4xy}=−\mathrm{19}<\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{this}\:\mathrm{case}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{system}\:\mathrm{has}\:\mathrm{four}\:\mathrm{roots}: \\ $$$$\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)\in\left\{\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}},\frac{\mathrm{5}−\sqrt{\mathrm{21}}}{\mathrm{2}}\right),\left(\frac{\mathrm{5}−\sqrt{\mathrm{21}}}{\mathrm{2}},\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}}\right)\right. \\ $$
Commented by 1549442205PVT last updated on 01/Aug/20
$$\mathrm{Ok},\mathrm{excuse}\:\mathrm{me}.\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 31/Jul/20
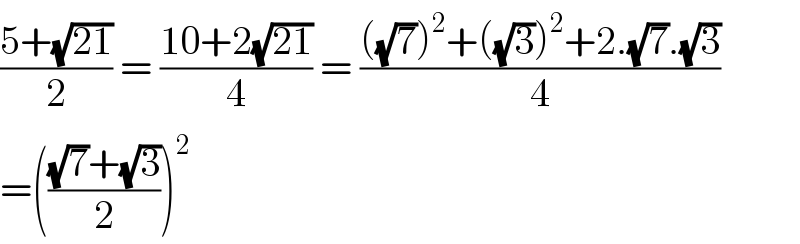
$$\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}}\:=\:\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{4}}\:=\:\frac{\left(\sqrt{\mathrm{7}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}.\sqrt{\mathrm{7}}.\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$=\left(\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$
