solve-the-inequalities-Q-1-1-log-a-2-x-1-log-a-x-gt-1-0-lt-a-lt-1-Q-2-log-x-4x-5-6-5x-lt-1-

Question Number 175335 by infinityaction last updated on 27/Aug/22

solve the inequalities

Q . (1) \frac{1 + \log_{a}^{2} x}{1 + \log_{a} x} > 1, 0 < a < 1

Q . (2) \log_{x} \frac{4 x + 5}{6 - 5 x} < - 1

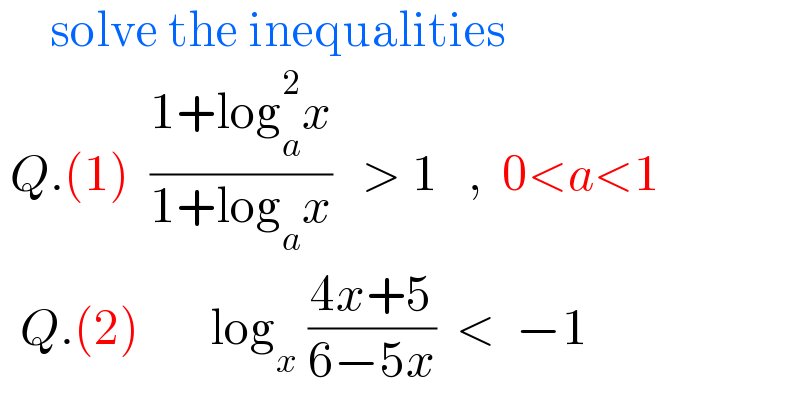
Answered by blackmamba last updated on 27/Aug/22

(1) x > 0

l e t \log_{a} x = t

\frac{1 + t^{2}}{1 + t} - \frac{1 + t}{1 + t} > 0

\frac{t^{2} - t}{t + 1} > 0 \Rightarrow \frac{t (t - 1)}{t + 1} > 0

- 1 < t < 0 \lor t > 1

- 1 < \log_{a} x < 0 \lor \log_{a} x > 1

\log_{a} (\frac{1}{a}) < \log_{a} x < \log_{a} 1 \lor \log_{a} x > \log_{a} a

1 < x < \frac{1}{a} \lor 0 < x < a

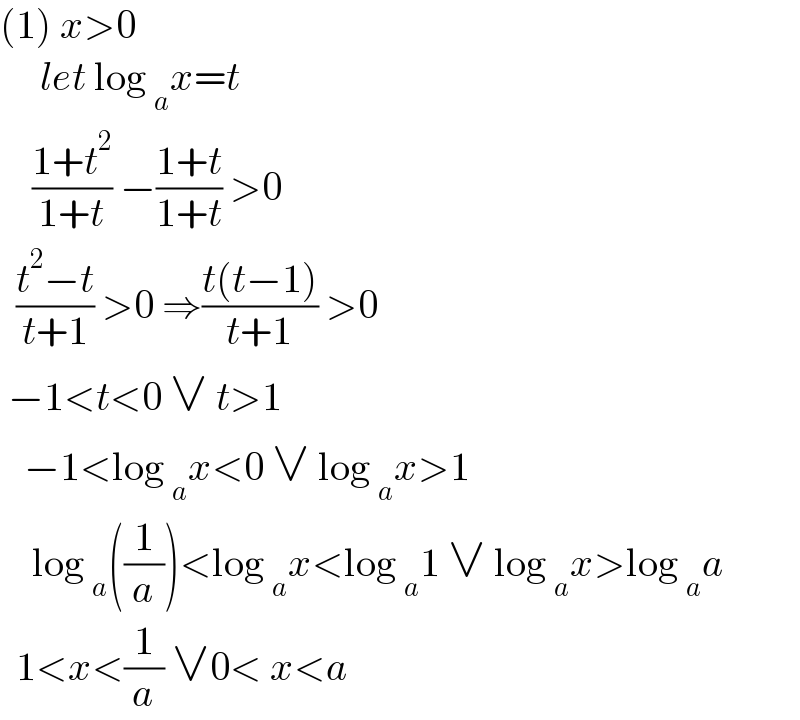
Commented by infinityaction last updated on 27/Aug/22

t h a n k s

Answered by mahdipoor last updated on 27/Aug/22

2 : i f a < b \Rightarrow {\begin{cases} c^{a} < c^{b} i f c ⩾ 1 \\ c^{a} > c^{b} i f 0 < c < 1 \end{cases}

\frac{4 x + 5}{6 - 5 x} > 0 \Rightarrow x \in (\frac{- 5}{4}, \frac{6}{5}) (i i i)

\Rightarrow\Rightarrow I : 0 < x < 1 (i)

x^{\land} ({l o g}_{x} \frac{4 x + 5}{6 - 5 x}) > x^{\land} (- 1) \Rightarrow \frac{4 x + 5}{6 - 5 x} > \frac{1}{x} \Rightarrow

4 x^{2} + 10 x - 6 > 0 \Rightarrow x \in R - [- 3, \frac{1}{2}] (i i)

i \cap i i \cap i i i = 0.5 < x < 1

\Rightarrow\Rightarrow II : 1 ⩽ x (i)

x^{\land} ({l o g}_{x} \frac{4 x + 5}{6 - 5 x}) ⩽ x^{\land} (- 1) \Rightarrow \frac{4 x + 5}{6 - 5 x} ⩽ \frac{1}{x} \Rightarrow

4 x^{2} + 10 x - 6 ⩽ 0 \Rightarrow x \in [- 3, \frac{1}{2}] (i i)

i \cap i i \cap i i i = ∄

I \cap II = 0.5 < x < 1

Commented by infinityaction last updated on 27/Aug/22

t h a n k s