Question Number 25965 by Chuks” last updated on 17/Dec/17

$${solve}\:{the}\:{integral} \\ $$$$\int\mathrm{sin}^{\mathrm{4}} \theta{d}\theta \\ $$
Answered by $@ty@m last updated on 17/Dec/17
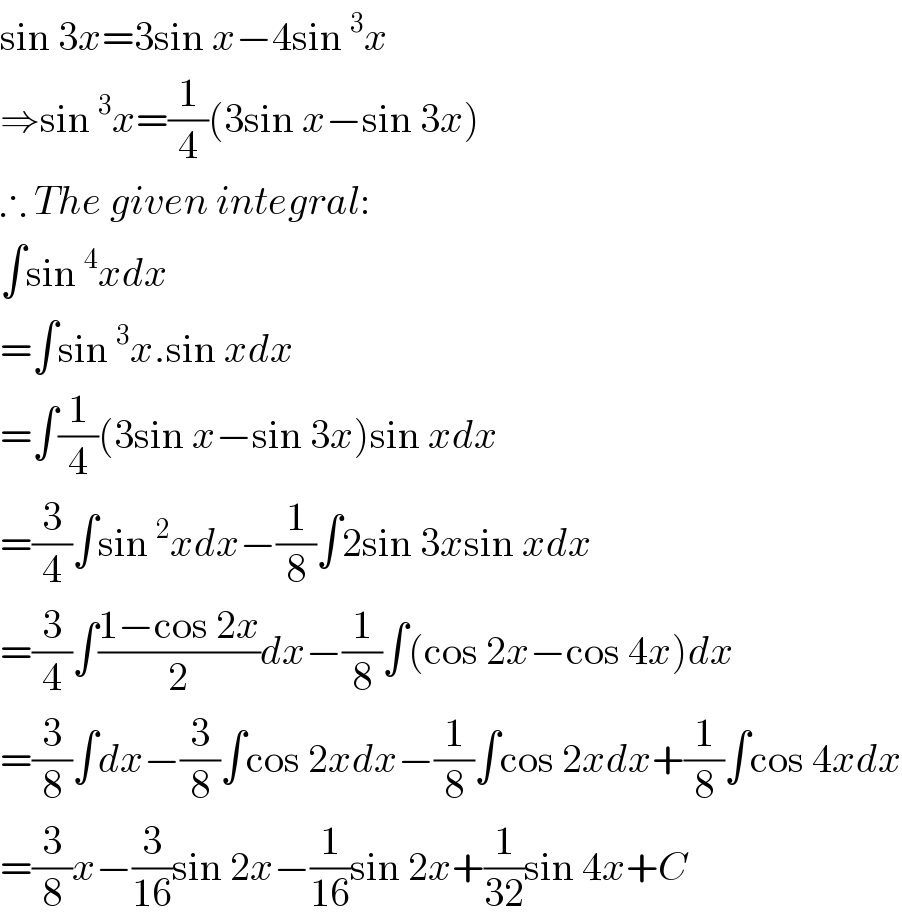
$$\mathrm{sin}\:\mathrm{3}{x}=\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x} \\ $$$$\Rightarrow\mathrm{sin}\:^{\mathrm{3}} {x}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}\right)\: \\ $$$$\therefore\:{The}\:{given}\:{integral}: \\ $$$$\int\mathrm{sin}\:^{\mathrm{4}} {xdx} \\ $$$$=\int\mathrm{sin}\:^{\mathrm{3}} {x}.\mathrm{sin}\:{xdx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3sin}\:{x}−\mathrm{sin}\:\mathrm{3}{x}\right)\mathrm{sin}\:{xdx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int\mathrm{sin}\:^{\mathrm{2}} {xdx}−\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{2sin}\:\mathrm{3}{x}\mathrm{sin}\:{xdx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}{dx}−\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{cos}\:\mathrm{2}{x}−\mathrm{cos}\:\mathrm{4}{x}\right){dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\int{dx}−\frac{\mathrm{3}}{\mathrm{8}}\int\mathrm{cos}\:\mathrm{2}{xdx}−\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{cos}\:\mathrm{2}{xdx}+\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{cos}\:\mathrm{4}{xdx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}{x}−\frac{\mathrm{3}}{\mathrm{16}}\mathrm{sin}\:\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\:\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\:\mathrm{4}{x}+{C} \\ $$
Commented by Chuks” last updated on 29/Dec/17

$${wow} \\ $$$$\boldsymbol{\mathrm{G}{reat}}\:\boldsymbol{{work}}.. \\ $$$$\boldsymbol{{More}}\:\boldsymbol{{knowledge}}\:\boldsymbol{{sir}} \\ $$
