Question Number 28705 by students last updated on 29/Jan/18

$${solve}\:{the}\:{integrayion}\:\frac{{sin}\mathrm{2}{x}}{{sin}\mathrm{5}{xsin}\mathrm{3}{x}} \\ $$
Answered by mrW2 last updated on 30/Jan/18
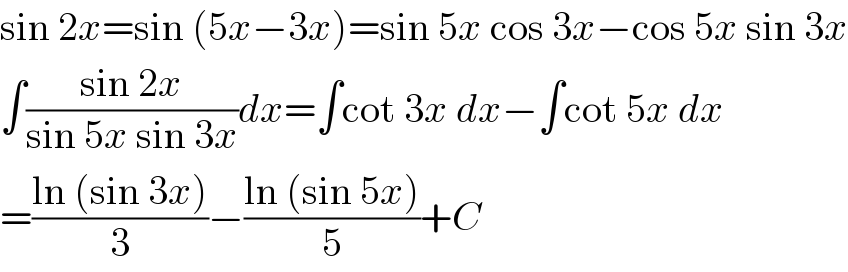
$$\mathrm{sin}\:\mathrm{2}{x}=\mathrm{sin}\:\left(\mathrm{5}{x}−\mathrm{3}{x}\right)=\mathrm{sin}\:\mathrm{5}{x}\:\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{5}{x}\:\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\int\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{5}{x}\:\mathrm{sin}\:\mathrm{3}{x}}{dx}=\int\mathrm{cot}\:\mathrm{3}{x}\:{dx}−\int\mathrm{cot}\:\mathrm{5}{x}\:{dx} \\ $$$$=\frac{\mathrm{ln}\:\left(\mathrm{sin}\:\mathrm{3}{x}\right)}{\mathrm{3}}−\frac{\mathrm{ln}\:\left(\mathrm{sin}\:\mathrm{5}{x}\right)}{\mathrm{5}}+{C} \\ $$
