Question Number 169051 by Mastermind last updated on 23/Apr/22

$${Solve}\:{the}\:{ODE} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}\right){y}'\:+\:{xy}\:=\:\mathrm{0},\:{with}\:{y}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$ \\ $$$${Mastermind} \\ $$
Commented by haladu last updated on 23/Apr/22
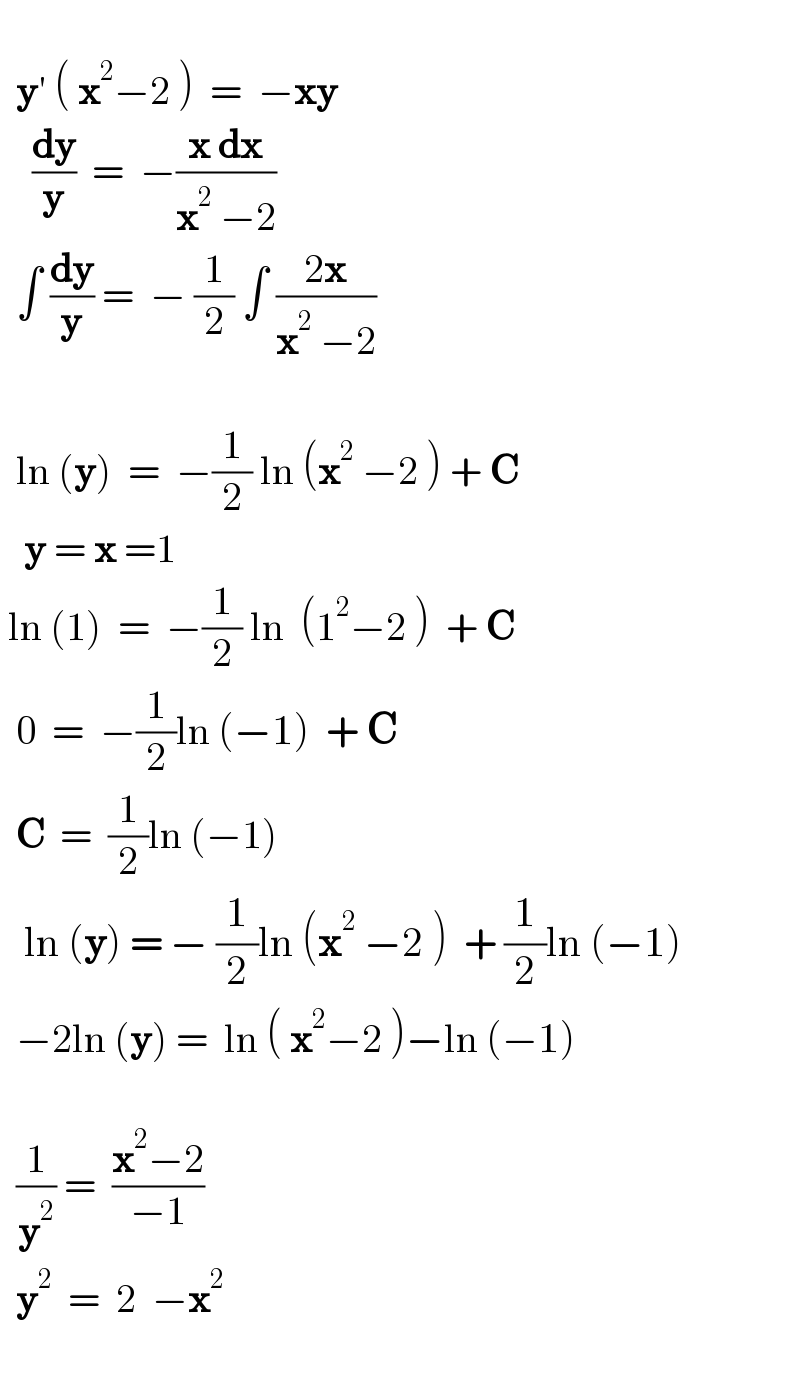
$$\:\: \\ $$$$\:\:\boldsymbol{\mathrm{y}}'\:\left(\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\:\right)\:\:=\:\:−\boldsymbol{\mathrm{xy}}\:\: \\ $$$$\:\:\:\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{y}}}\:\:=\:\:−\frac{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\mathrm{2}} \\ $$$$\:\:\int\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{y}}}\:=\:\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{2}\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\mathrm{2}} \\ $$$$\:\: \\ $$$$\:\:\mathrm{ln}\:\left(\boldsymbol{\mathrm{y}}\right)\:\:=\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\mathrm{2}\:\right)\:+\:\boldsymbol{\mathrm{C}} \\ $$$$\:\:\:\boldsymbol{\mathrm{y}}\:=\:\boldsymbol{\mathrm{x}}\:=\mathrm{1}\:\: \\ $$$$\:\mathrm{ln}\:\left(\mathrm{1}\right)\:\:=\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\:\left(\mathrm{1}^{\mathrm{2}} −\mathrm{2}\:\right)\:\:+\:\boldsymbol{\mathrm{C}} \\ $$$$\:\:\mathrm{0}\:\:=\:\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(−\mathrm{1}\right)\:\:+\:\boldsymbol{\mathrm{C}}\: \\ $$$$\:\:\boldsymbol{\mathrm{C}}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(−\mathrm{1}\right) \\ $$$$\:\:\:\mathrm{ln}\:\left(\boldsymbol{\mathrm{y}}\right)\:=\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\mathrm{2}\:\right)\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(−\mathrm{1}\right) \\ $$$$\:\:−\mathrm{2ln}\:\left(\boldsymbol{\mathrm{y}}\right)\:=\:\:\mathrm{ln}\:\left(\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\:\right)−\mathrm{ln}\:\left(−\mathrm{1}\right) \\ $$$$\:\:\: \\ $$$$\:\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\:=\:\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}}{−\mathrm{1}}\:\: \\ $$$$\:\:\boldsymbol{\mathrm{y}}^{\mathrm{2}} \:\:=\:\:\mathrm{2}\:\:−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \: \\ $$$$ \\ $$
Commented by Mastermind last updated on 23/Apr/22

$${Could}\:{you}\:{please}\:{recheck}\:{your}\:{solution}? \\ $$
Commented by haladu last updated on 23/Apr/22

$$\:\boldsymbol{{yes}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{was}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{hurry}}\:\boldsymbol{\mathrm{becuse}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{was}}\:\boldsymbol{\mathrm{time}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{sallat}}. \\ $$
Commented by Mastermind last updated on 24/Apr/22

$${Okay}\:{i}\:{understand} \\ $$
Answered by Mathspace last updated on 23/Apr/22

$$\left({x}^{\mathrm{2}} −\mathrm{2}\right){y}^{'} +{xy}=\mathrm{0}\:\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{2}\right){y}^{'} =−{xy}\:\Rightarrow \\ $$$$\frac{{y}^{'} }{{y}}=−\frac{{x}}{{x}^{\mathrm{2}} −\mathrm{2}}\:\Rightarrow{ln}\mid{y}\mid=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −\mathrm{2}\mid\:+{c} \\ $$$$\Rightarrow{y}=\frac{{k}}{\:\sqrt{\mid{x}^{\mathrm{2}} −\mathrm{2}\mid}} \\ $$$${solution}\:{on}\:{w}=\left\{{x}/{x}^{\mathrm{2}} −\mathrm{2}<\mathrm{0}\right\} \\ $$$$\Rightarrow{y}=\frac{{k}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}={k}\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow{y}^{'} ={k}^{'} \left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} +{k}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}{x}\right)\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$={k}^{'} \left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} +{xk}\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\left({e}\right)\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{2}\right){k}^{'} \left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$−{xk}\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:+{xk}\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{0}\Rightarrow{k}^{'} =\mathrm{0}\:\Rightarrow{k}=\lambda\:\Rightarrow \\ $$$${y}\left({x}\right)=\frac{\lambda}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }} \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{1}\:\Rightarrow\lambda=\mathrm{1}\:\Rightarrow{y}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }} \\ $$
Commented by Mastermind last updated on 24/Apr/22

$${Sir},\:{i}\:{think}\:{answer}\:{is}\:{y}=\frac{{i}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}}} \\ $$
Commented by Mathspace last updated on 24/Apr/22

$${no} \\ $$
