Question Number 169050 by Mastermind last updated on 23/Apr/22
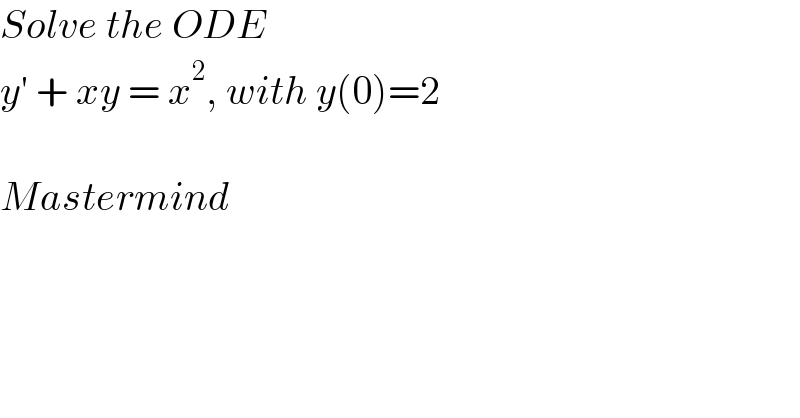
$${Solve}\:{the}\:{ODE} \\ $$$${y}'\:+\:{xy}\:=\:{x}^{\mathrm{2}} ,\:{with}\:{y}\left(\mathrm{0}\right)=\mathrm{2} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by Mathspace last updated on 23/Apr/22
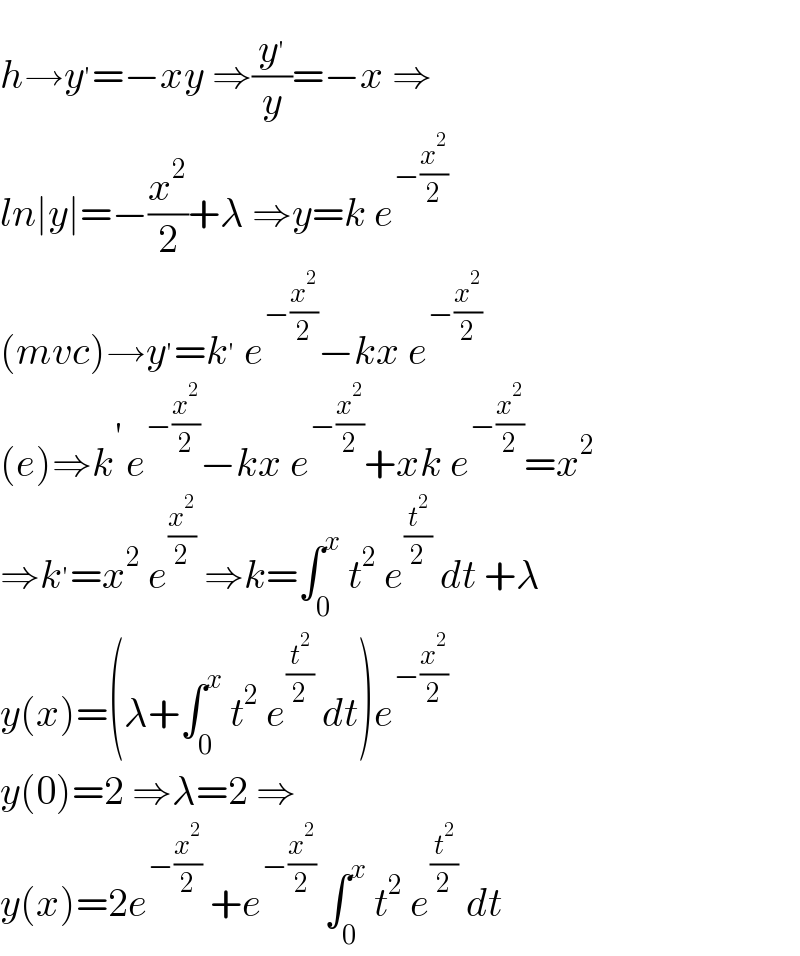
$${h}\rightarrow{y}^{'} =−{xy}\:\Rightarrow\frac{{y}^{'} }{{y}}=−{x}\:\Rightarrow \\ $$$${ln}\mid{y}\mid=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\lambda\:\Rightarrow{y}={k}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\left({mvc}\right)\rightarrow{y}^{'} ={k}^{'} \:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −{kx}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\left({e}\right)\Rightarrow{k}^{'\:} {e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −{kx}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +{xk}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} ={x}^{\mathrm{2}} \\ $$$$\Rightarrow{k}^{'} ={x}^{\mathrm{2}} \:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow{k}=\int_{\mathrm{0}} ^{{x}} \:{t}^{\mathrm{2}} \:{e}^{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} \:{dt}\:+\lambda \\ $$$${y}\left({x}\right)=\left(\lambda+\int_{\mathrm{0}} ^{{x}} \:{t}^{\mathrm{2}} \:{e}^{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} \:{dt}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{2}\:\Rightarrow\lambda=\mathrm{2}\:\Rightarrow \\ $$$${y}\left({x}\right)=\mathrm{2}{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:+{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\int_{\mathrm{0}} ^{{x}} \:{t}^{\mathrm{2}} \:{e}^{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} \:{dt} \\ $$
Commented by Mastermind last updated on 24/Apr/22
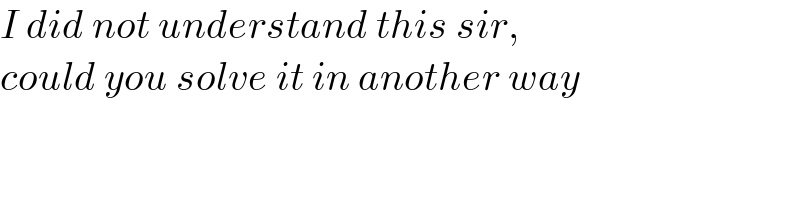
$${I}\:{did}\:{not}\:{understand}\:{this}\:{sir}, \\ $$$${could}\:{you}\:{solve}\:{it}\:{in}\:{another}\:{way} \\ $$$$ \\ $$
