Menu Close

solve-the-simultaenous-equation-x-y-3-2-x-x-2-y-y-find-xand-y-show-ur-workings-

Tinku Tara 0 Comments
Pin




Question Number 17017 by Mr easymsn last updated on 29/Jun/17
solve the simultaenous equation x+y=3 (2^x /x)=(2^y /y) find xand y.show ur workings....
$${solve}\:{the}\:{simultaenous}\:{equation} \\ $$$$\:{x}+{y}=\mathrm{3} \\ $$$$\:\frac{\mathrm{2}^{{x}} }{{x}}=\frac{\mathrm{2}^{{y}} }{{y}} \\ $$$$\:{find}\:{xand}\:{y}.{show}\:{ur}\:{workings}…. \\ $$
Answered by mrW1 last updated on 30/Jun/17
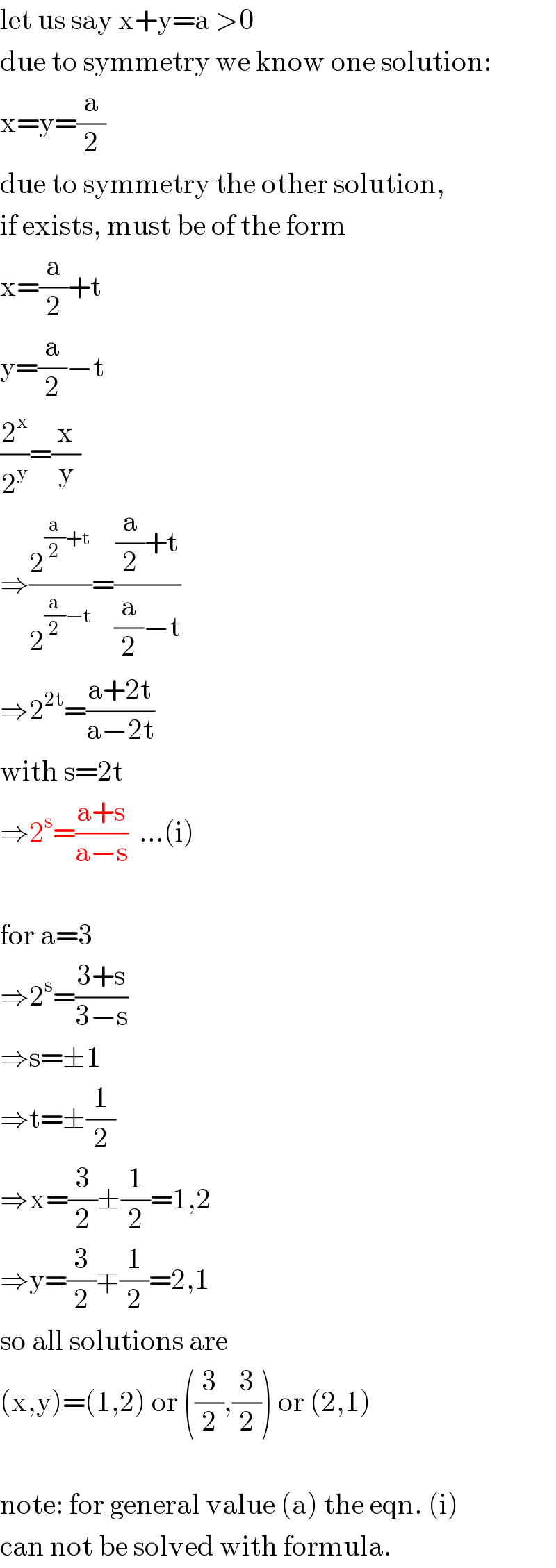
let us say x+y=a >0 due to symmetry we know one solution: x=y=(a/2) due to symmetry the other solution, if exists, must be of the form x=(a/2)+t y=(a/2)−t (2^x /2^y )=(x/y) ⇒(2^((a/2)+t) /2^((a/2)−t) )=(((a/2)+t)/((a/2)−t)) ⇒2^(2t) =((a+2t)/(a−2t)) with s=2t ⇒2^s =((a+s)/(a−s)) ...(i) for a=3 ⇒2^s =((3+s)/(3−s)) ⇒s=±1 ⇒t=±(1/2) ⇒x=(3/2)±(1/2)=1,2 ⇒y=(3/2)∓(1/2)=2,1 so all solutions are (x,y)=(1,2) or ((3/2),(3/2)) or (2,1) note: for general value (a) the eqn. (i) can not be solved with formula.
$$\mathrm{let}\:\mathrm{us}\:\mathrm{say}\:\mathrm{x}+\mathrm{y}=\mathrm{a}\:>\mathrm{0} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\mathrm{we}\:\mathrm{know}\:\mathrm{one}\:\mathrm{solution}: \\ $$$$\mathrm{x}=\mathrm{y}=\frac{\mathrm{a}}{\mathrm{2}} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\mathrm{the}\:\mathrm{other}\:\mathrm{solution}, \\ $$$$\mathrm{if}\:\mathrm{exists},\:\mathrm{must}\:\mathrm{be}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$$\mathrm{x}=\frac{\mathrm{a}}{\mathrm{2}}+\mathrm{t} \\ $$$$\mathrm{y}=\frac{\mathrm{a}}{\mathrm{2}}−\mathrm{t} \\ $$$$\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{2}^{\mathrm{y}} }=\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\Rightarrow\frac{\mathrm{2}^{\frac{\mathrm{a}}{\mathrm{2}}+\mathrm{t}} }{\mathrm{2}^{\frac{\mathrm{a}}{\mathrm{2}}−\mathrm{t}} }=\frac{\frac{\mathrm{a}}{\mathrm{2}}+\mathrm{t}}{\frac{\mathrm{a}}{\mathrm{2}}−\mathrm{t}} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{2t}} =\frac{\mathrm{a}+\mathrm{2t}}{\mathrm{a}−\mathrm{2t}} \\ $$$$\mathrm{with}\:\mathrm{s}=\mathrm{2t} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{s}} =\frac{\mathrm{a}+\mathrm{s}}{\mathrm{a}−\mathrm{s}}\:\:…\left(\mathrm{i}\right) \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{a}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{s}} =\frac{\mathrm{3}+\mathrm{s}}{\mathrm{3}−\mathrm{s}} \\ $$$$\Rightarrow\mathrm{s}=\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{t}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1},\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{3}}{\mathrm{2}}\mp\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2},\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{are} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{1},\mathrm{2}\right)\:\mathrm{or}\:\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\:\mathrm{or}\:\left(\mathrm{2},\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{note}:\:\mathrm{for}\:\mathrm{general}\:\mathrm{value}\:\left(\mathrm{a}\right)\:\mathrm{the}\:\mathrm{eqn}.\:\left(\mathrm{i}\right) \\ $$$$\mathrm{can}\:\mathrm{not}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{with}\:\mathrm{formula}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *