Question Number 45280 by peter frank last updated on 11/Oct/18
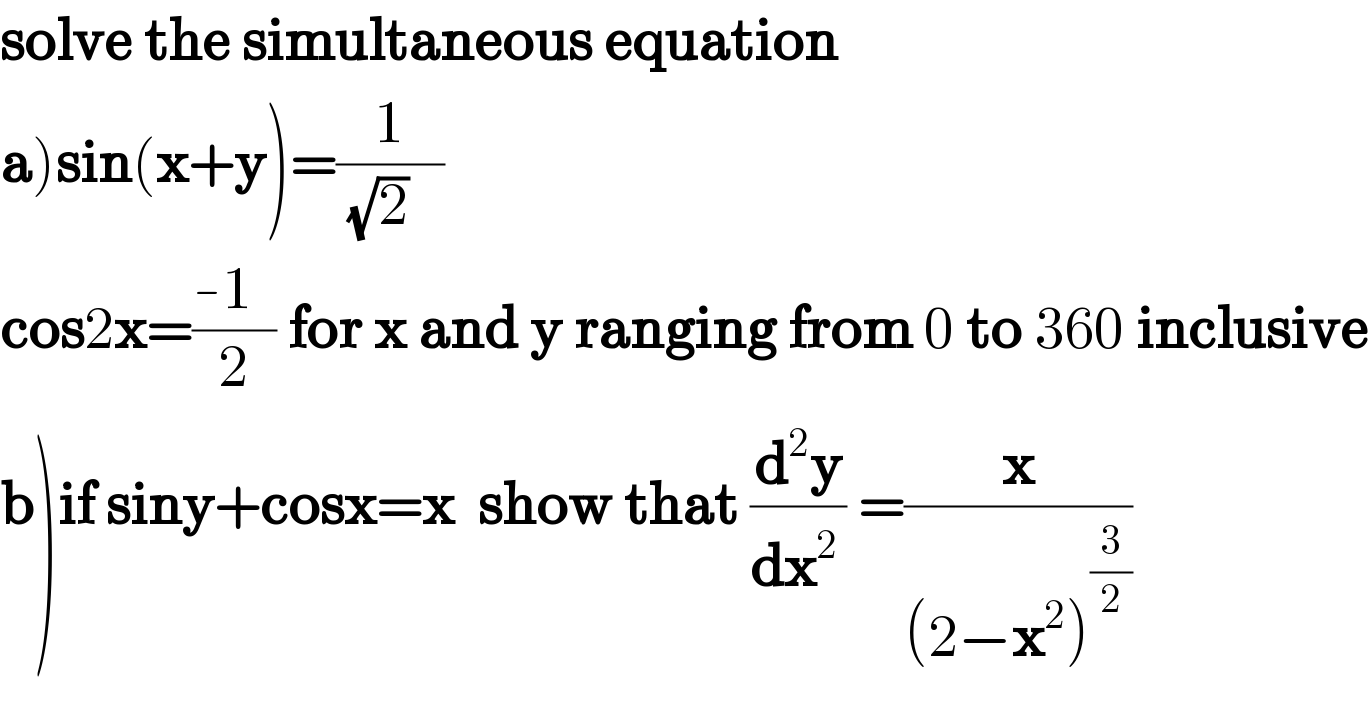
$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{simultaneous}}\:\boldsymbol{\mathrm{equation}} \\ $$$$\left.\boldsymbol{\mathrm{a}}\right)\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\:\:} \\ $$$$\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{\mathrm{x}}=\frac{-\mathrm{1}\:\:}{\mathrm{2}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{ranging}}\:\boldsymbol{\mathrm{from}}\:\mathrm{0}\:\boldsymbol{\mathrm{to}}\:\mathrm{360}\:\boldsymbol{\mathrm{inclusive}} \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{siny}}+\boldsymbol{\mathrm{cosx}}=\boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}}\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}\:} }\:=\frac{\boldsymbol{\mathrm{x}}}{\left(\mathrm{2}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Oct/18
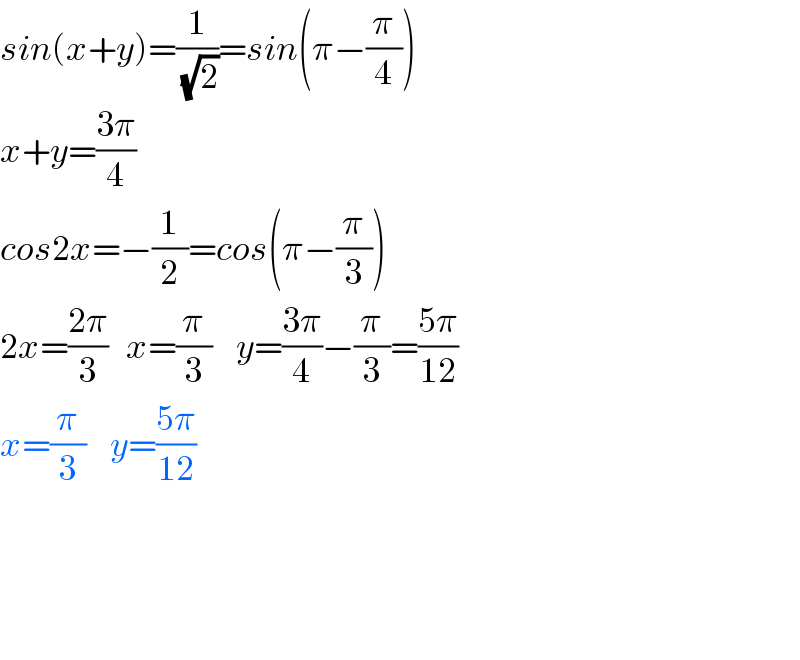
$${sin}\left({x}+{y}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}={sin}\left(\pi−\frac{\pi}{\mathrm{4}}\right) \\ $$$${x}+{y}=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$${cos}\mathrm{2}{x}=−\frac{\mathrm{1}}{\mathrm{2}}={cos}\left(\pi−\frac{\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{2}{x}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:\:\:{x}=\frac{\pi}{\mathrm{3}}\:\:\:\:{y}=\frac{\mathrm{3}\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{3}}=\frac{\mathrm{5}\pi}{\mathrm{12}} \\ $$$${x}=\frac{\pi}{\mathrm{3}}\:\:\:\:{y}=\frac{\mathrm{5}\pi}{\mathrm{12}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by peter frank last updated on 11/Oct/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{pls}\:\mathrm{help}\:\mathrm{qn2} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18
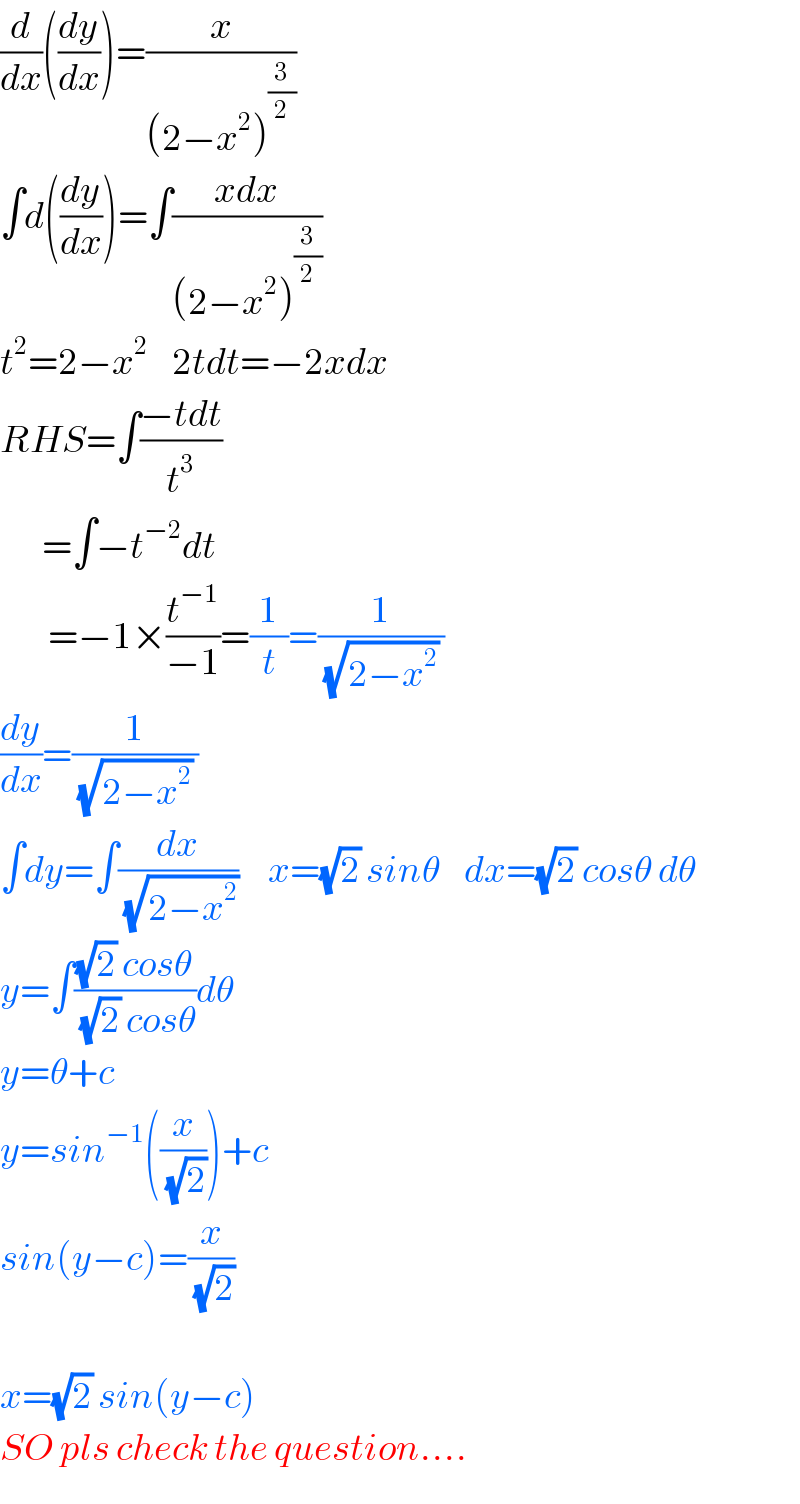
$$\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{x}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\int{d}\left(\frac{{dy}}{{dx}}\right)=\int\frac{{xdx}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${t}^{\mathrm{2}} =\mathrm{2}−{x}^{\mathrm{2}} \:\:\:\:\mathrm{2}{tdt}=−\mathrm{2}{xdx} \\ $$$${RHS}=\int\frac{−{tdt}}{{t}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:=\int−{t}^{−\mathrm{2}} {dt} \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{1}×\frac{{t}^{−\mathrm{1}} }{−\mathrm{1}}=\frac{\mathrm{1}}{{t}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }\:} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }\:} \\ $$$$\int{dy}=\int\frac{{dx}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}\:\:\:\:\:{x}=\sqrt{\mathrm{2}}\:{sin}\theta\:\:\:\:{dx}=\sqrt{\mathrm{2}}\:{cos}\theta\:{d}\theta \\ $$$${y}=\int\frac{\sqrt{\mathrm{2}}\:{cos}\theta}{\:\sqrt{\mathrm{2}}\:{cos}\theta}{d}\theta \\ $$$${y}=\theta+{c} \\ $$$${y}={sin}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+{c} \\ $$$${sin}\left({y}−{c}\right)=\frac{{x}}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$${x}=\sqrt{\mathrm{2}}\:{sin}\left({y}−{c}\right) \\ $$$${SO}\:{pls}\:{check}\:{the}\:{question}…. \\ $$
Commented by peter frank last updated on 12/Oct/18
$$\mathrm{its}\:\mathrm{seem}\:\mathrm{there}\:\mathrm{are}\:\mathrm{something}\:\mathrm{wrong}.\mathrm{thanks}\:\mathrm{sir} \\ $$$$ \\ $$
