Question Number 110087 by 1549442205PVT last updated on 27/Aug/20
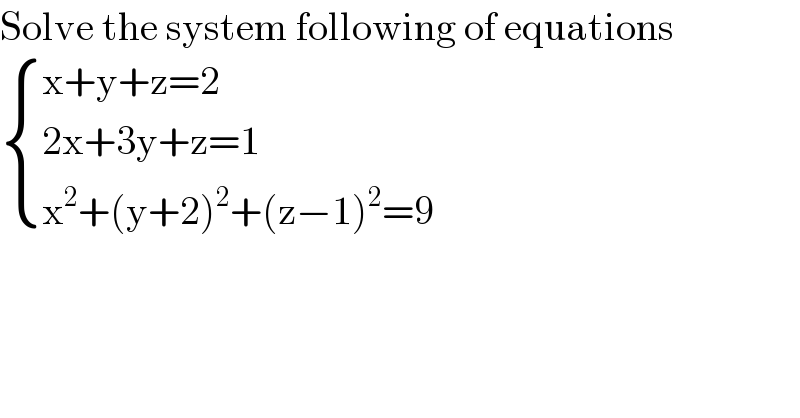
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}\:\mathrm{following}\:\mathrm{of}\:\mathrm{equations} \\ $$$$\begin{cases}{\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{2}}\\{\mathrm{2x}+\mathrm{3y}+\mathrm{z}=\mathrm{1}}\\{\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{9}}\end{cases} \\ $$
Commented by bemath last updated on 27/Aug/20
![[△((be)/(math))▽] { ((x+y+z = 2)),((2x+3y+z = 1)),((x^2 +(y+2)^2 +(z−1)^2 = 9)) :} ⇒z = z ⇒2−x−y=1−2x−3y ⇒ x+2y=−1 ⇒ (−1−2y)^2 +(y+2)^2 +(2x+3y)^2 =9 (1+2y)^2 +(y+2)^2 +(−2−y)^2 =9 2(y+2)^2 +(1+2y)^2 =9 2(y^2 +4y+4)+4y^2 +4y+1=9 6y^2 +12y=0→6y(y+2)=0 y=0 or y=−2 case(1) y=0→ { ((x=−1)),((z=3)) :} case(2) y=−2→ { ((x=3)),((z=1)) :} solution set is {(−1,0,3),(3,−2,1)}](https://www.tinkutara.com/question/Q110100.png)
$$\:\:\:\left[\bigtriangleup\frac{{be}}{{math}}\bigtriangledown\right] \\ $$$$\begin{cases}{{x}+{y}+{z}\:=\:\mathrm{2}}\\{\mathrm{2}{x}+\mathrm{3}{y}+{z}\:=\:\mathrm{1}}\\{{x}^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} +\left({z}−\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{9}}\end{cases} \\ $$$$\Rightarrow{z}\:=\:{z}\:\Rightarrow\mathrm{2}−{x}−{y}=\mathrm{1}−\mathrm{2}{x}−\mathrm{3}{y} \\ $$$$\Rightarrow\:{x}+\mathrm{2}{y}=−\mathrm{1} \\ $$$$\Rightarrow\:\left(−\mathrm{1}−\mathrm{2}{y}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}+\mathrm{3}{y}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\left(\mathrm{1}+\mathrm{2}{y}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} +\left(−\mathrm{2}−{y}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{2}\left({y}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{2}{y}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{2}\left({y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{4}\right)+\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{1}=\mathrm{9} \\ $$$$\mathrm{6}{y}^{\mathrm{2}} +\mathrm{12}{y}=\mathrm{0}\rightarrow\mathrm{6}{y}\left({y}+\mathrm{2}\right)=\mathrm{0} \\ $$$${y}=\mathrm{0}\:{or}\:{y}=−\mathrm{2} \\ $$$${case}\left(\mathrm{1}\right)\:{y}=\mathrm{0}\rightarrow\begin{cases}{{x}=−\mathrm{1}}\\{{z}=\mathrm{3}}\end{cases} \\ $$$${case}\left(\mathrm{2}\right)\:{y}=−\mathrm{2}\rightarrow\begin{cases}{{x}=\mathrm{3}}\\{{z}=\mathrm{1}}\end{cases} \\ $$$${solution}\:{set}\:{is}\:\left\{\left(−\mathrm{1},\mathrm{0},\mathrm{3}\right),\left(\mathrm{3},−\mathrm{2},\mathrm{1}\right)\right\} \\ $$$$ \\ $$
Commented by john santu last updated on 27/Aug/20

$${nice}\: \\ $$
Commented by 1549442205PVT last updated on 28/Aug/20

$$\mathrm{Thank}\:\mathrm{you} \\ $$
