Question Number 115909 by Eric002 last updated on 29/Sep/20
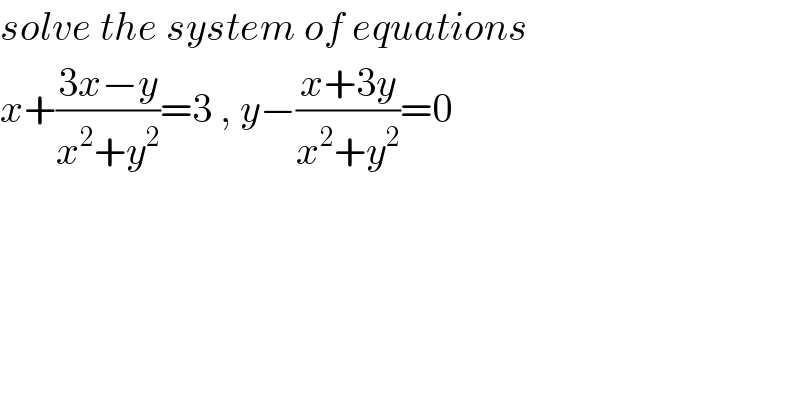
$${solve}\:{the}\:{system}\:{of}\:{equations} \\ $$$${x}+\frac{\mathrm{3}{x}−{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\mathrm{3}\:,\:{y}−\frac{{x}+\mathrm{3}{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\mathrm{0} \\ $$
Answered by MJS_new last updated on 29/Sep/20
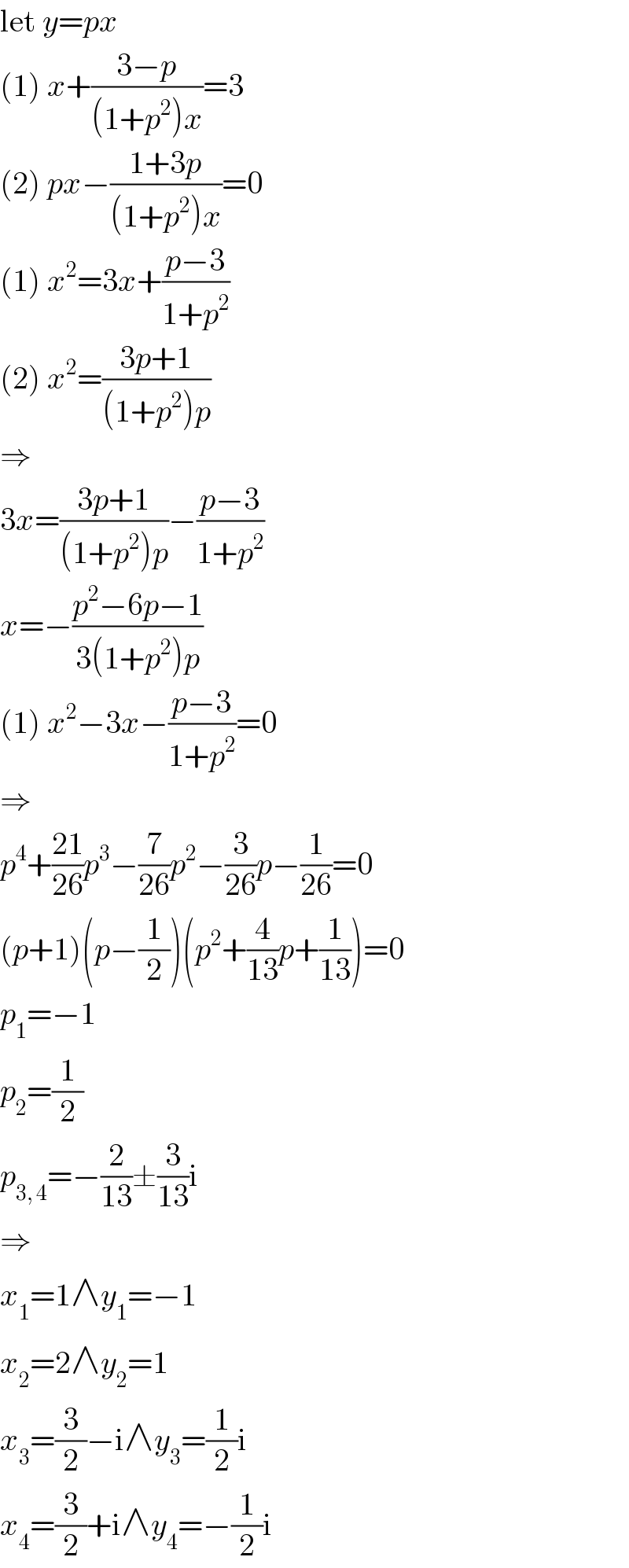
$$\mathrm{let}\:{y}={px} \\ $$$$\left(\mathrm{1}\right)\:{x}+\frac{\mathrm{3}−{p}}{\left(\mathrm{1}+{p}^{\mathrm{2}} \right){x}}=\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:{px}−\frac{\mathrm{1}+\mathrm{3}{p}}{\left(\mathrm{1}+{p}^{\mathrm{2}} \right){x}}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} =\mathrm{3}{x}+\frac{{p}−\mathrm{3}}{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} =\frac{\mathrm{3}{p}+\mathrm{1}}{\left(\mathrm{1}+{p}^{\mathrm{2}} \right){p}} \\ $$$$\Rightarrow \\ $$$$\mathrm{3}{x}=\frac{\mathrm{3}{p}+\mathrm{1}}{\left(\mathrm{1}+{p}^{\mathrm{2}} \right){p}}−\frac{{p}−\mathrm{3}}{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$$${x}=−\frac{{p}^{\mathrm{2}} −\mathrm{6}{p}−\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{p}^{\mathrm{2}} \right){p}} \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} −\mathrm{3}{x}−\frac{{p}−\mathrm{3}}{\mathrm{1}+{p}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${p}^{\mathrm{4}} +\frac{\mathrm{21}}{\mathrm{26}}{p}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{26}}{p}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{26}}{p}−\frac{\mathrm{1}}{\mathrm{26}}=\mathrm{0} \\ $$$$\left({p}+\mathrm{1}\right)\left({p}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({p}^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{13}}{p}+\frac{\mathrm{1}}{\mathrm{13}}\right)=\mathrm{0} \\ $$$${p}_{\mathrm{1}} =−\mathrm{1} \\ $$$${p}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}_{\mathrm{3},\:\mathrm{4}} =−\frac{\mathrm{2}}{\mathrm{13}}\pm\frac{\mathrm{3}}{\mathrm{13}}\mathrm{i} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\mathrm{1}\wedge{y}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}\wedge{y}_{\mathrm{2}} =\mathrm{1} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{i}\wedge{y}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i} \\ $$$${x}_{\mathrm{4}} =\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{i}\wedge{y}_{\mathrm{4}} =−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i} \\ $$
