Question Number 162181 by bobhans last updated on 27/Dec/21
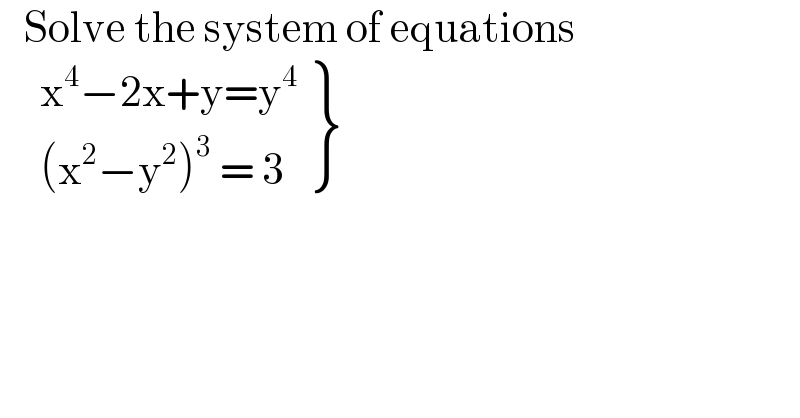
$$\:\:\:\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}\: \\ $$$$\:\:\:\:\:\left.\begin{matrix}{\mathrm{x}^{\mathrm{4}} −\mathrm{2x}+\mathrm{y}=\mathrm{y}^{\mathrm{4}} }\\{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{3}} \:=\:\mathrm{3}}\end{matrix}\right\}\: \\ $$
Commented by benhamimed last updated on 27/Dec/21

$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)−\mathrm{2}{x}+{y}=\mathrm{0} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{3}}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{x}+{y}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\frac{\mathrm{2}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}}{x}+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}}{y}=\mathrm{0} \\ $$$$\left({x}−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{1}}{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{3}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{6}}}+\frac{\mathrm{1}}{\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{6}}} \\ $$$$\left({x}−\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{3}}\right)^{\mathrm{2}} +\left({y}+\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{12}}\right)^{\mathrm{2}} =\frac{\mathrm{5}\sqrt[{\mathrm{3}}]{\mathrm{36}}}{\mathrm{24}} \\ $$$${les}\:{solution}\:{de}\:{system}\:{sont}\:{l}\:'{ensemble} \\ $$$${des}\:{points}\:{qui}\:{forment}\:{un}\:{cercle}\:\left({C}\right) \\ $$$${de}\:{centre}\:\left(\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{3}};\frac{−\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{12}}\right)\:{et}\:{demi}\:{rayon}\:\frac{\sqrt{\mathrm{30}}.\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{12}} \\ $$$$ \\ $$
Answered by cortano last updated on 28/Dec/21

