Question Number 151115 by mathdanisur last updated on 18/Aug/21
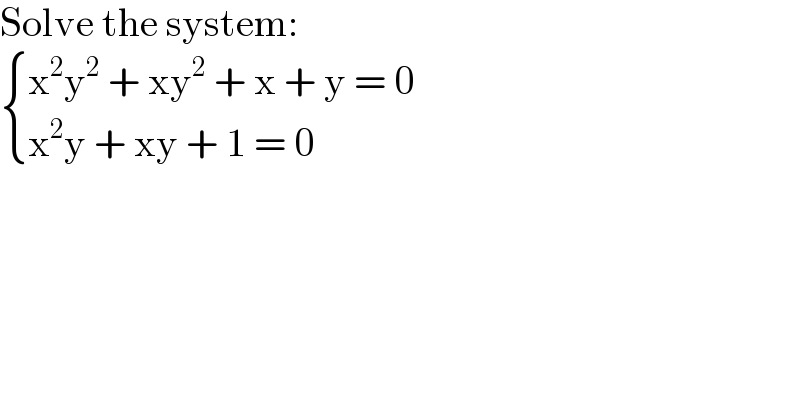
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \:+\:\mathrm{xy}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{y}\:=\:\mathrm{0}}\\{\mathrm{x}^{\mathrm{2}} \mathrm{y}\:+\:\mathrm{xy}\:+\:\mathrm{1}\:=\:\mathrm{0}}\end{cases} \\ $$
Answered by dumitrel last updated on 18/Aug/21
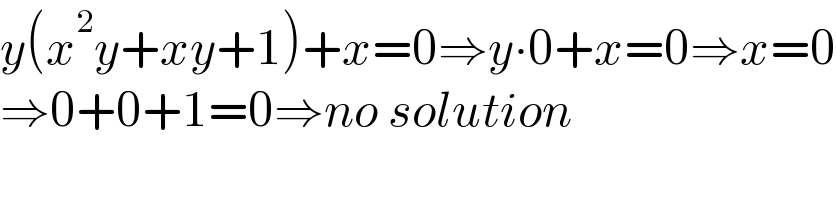
$${y}\left({x}^{\mathrm{2}} {y}+{xy}+\mathrm{1}\right)+{x}=\mathrm{0}\Rightarrow{y}\centerdot\mathrm{0}+{x}=\mathrm{0}\Rightarrow{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{0}+\mathrm{0}+\mathrm{1}=\mathrm{0}\Rightarrow{no}\:{solution} \\ $$
Commented by mathdanisur last updated on 18/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Aug/21
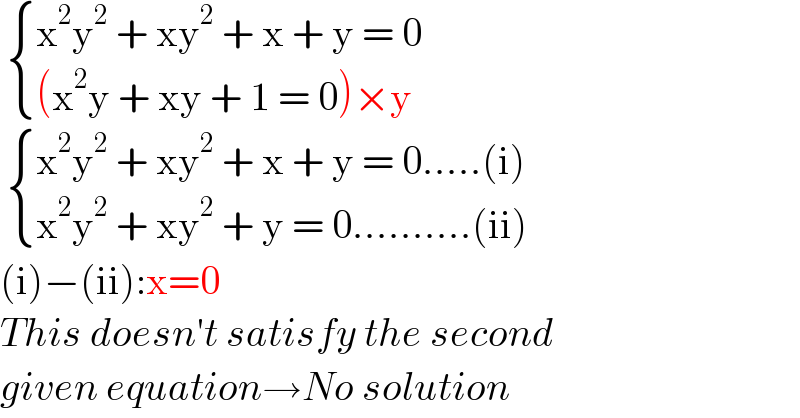
$$\:\begin{cases}{\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \:+\:\mathrm{xy}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{y}\:=\:\mathrm{0}}\\{\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}\:+\:\mathrm{xy}\:+\:\mathrm{1}\:=\:\mathrm{0}\right)×\mathrm{y}}\end{cases} \\ $$$$\:\begin{cases}{\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \:+\:\mathrm{xy}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{y}\:=\:\mathrm{0}…..\left(\mathrm{i}\right)}\\{\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \:+\:\mathrm{xy}^{\mathrm{2}} \:+\:\mathrm{y}\:=\:\mathrm{0}……….\left(\mathrm{ii}\right)}\end{cases} \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right):\mathrm{x}=\mathrm{0} \\ $$$${This}\:{doesn}'{t}\:{satisfy}\:{the}\:{second} \\ $$$${given}\:{equation}\rightarrow{No}\:{solution} \\ $$
Commented by mathdanisur last updated on 18/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\mathrm{Ser} \\ $$
Answered by Olaf_Thorendsen last updated on 18/Aug/21
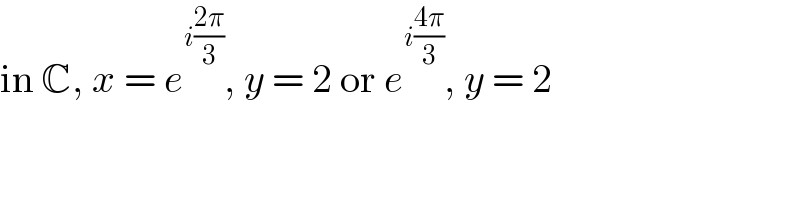
$$\mathrm{in}\:\mathbb{C},\:{x}\:=\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} ,\:{y}\:=\:\mathrm{2}\:\mathrm{or}\:{e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} ,\:{y}\:=\:\mathrm{2} \\ $$
Commented by MJS_new last updated on 18/Aug/21

$$\mathrm{how}? \\ $$
