Menu Close

solve-this-2-sinx-cosx-2-3sinx-sin-2x-dx-

Tinku Tara 0 Comments
Pin




Question Number 48104 by wasim last updated on 19/Nov/18
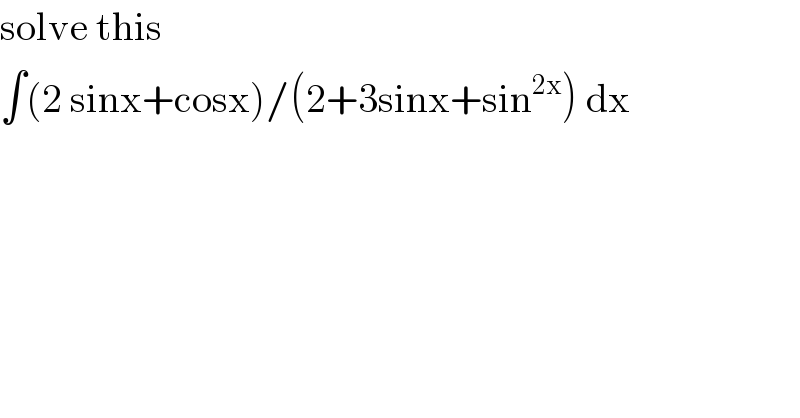
solve this ∫(2 sinx+cosx)/(2+3sinx+sin^(2x) ) dx
$$\mathrm{solve}\:\mathrm{this}\:\: \\ $$$$\int\left(\mathrm{2}\:\mathrm{sinx}+\mathrm{cosx}\right)/\left(\mathrm{2}+\mathrm{3sinx}+\mathrm{sin}^{\mathrm{2x}} \right)\:\mathrm{dx} \\ $$
Answered by MJS last updated on 19/Nov/18
Weierstrass−substitution t=tan (x/2) ⇒ x=2arctan t; dx=((2dt)/(1+t^2 )) sin x =((2t)/(1+t^2 )); cos x =((1−t^2 )/(1+t^2 )) −∫((t^2 −4t−1)/((t+1)^2 (t^2 +t+1)))dt= =2∫(dt/(t+1))−4∫(dt/((t+1)^2 ))−∫((2t−3)/(t^2 +t+1))dt= =2∫(dt/(t+1))−4∫(dt/((t+1)^2 ))−∫((2x+1)/(t^2 +t+1))dt+4∫(dt/(t^2 +t+1)) =2ln (t+1) +(4/(t+1))−ln (t^2 +t+1) +((8(√3))/3)arctan (((√3)/3)(2t+1)) = =ln (((t+1)^2 )/(t^2 +t+1)) +(4/(t+1))+((8(√3))/3)arctan (((√3)/3)(2t+1)) = =ln ((1+sin x)/(2+sin x)) +ln 2 +2+2sec x −2tan x +((8(√3))/3)arctan (((√3)/3)(1+2tan (x/2))) = =ln ((1+sin x)/(2+sin x)) +2sec x −2tan x +((8(√3))/3)arctan (((√3)/3)(1+2tan (x/2))) +C
$$\mathrm{Weierstrass}−\mathrm{substitution} \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Rightarrow\:{x}=\mathrm{2arctan}\:{t};\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$−\int\frac{{t}^{\mathrm{2}} −\mathrm{4}{t}−\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{dt}= \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}+\mathrm{1}}−\mathrm{4}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\int\frac{\mathrm{2}{t}−\mathrm{3}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}+\mathrm{1}}−\mathrm{4}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\int\frac{\mathrm{2}{x}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}+\mathrm{4}\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}} \\ $$$$=\mathrm{2ln}\:\left({t}+\mathrm{1}\right)\:+\frac{\mathrm{4}}{{t}+\mathrm{1}}−\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:+\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)\right)\:= \\ $$$$=\mathrm{ln}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:+\frac{\mathrm{4}}{{t}+\mathrm{1}}+\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)\right)\:= \\ $$$$=\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{2}+\mathrm{sin}\:{x}}\:+\mathrm{ln}\:\mathrm{2}\:+\mathrm{2}+\mathrm{2sec}\:{x}\:−\mathrm{2tan}\:{x}\:+\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{1}+\mathrm{2tan}\:\frac{{x}}{\mathrm{2}}\right)\right)\:= \\ $$$$=\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{2}+\mathrm{sin}\:{x}}\:+\mathrm{2sec}\:{x}\:−\mathrm{2tan}\:{x}\:+\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{1}+\mathrm{2tan}\:\frac{{x}}{\mathrm{2}}\right)\right)\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *