solve-x-1-2-x-3-

Question Number 126180 by benjo_mathlover last updated on 18/Dec/20

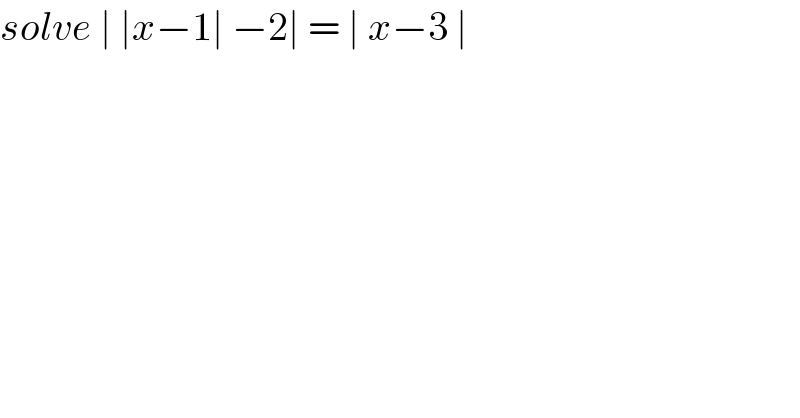
$${solve}\:\mid\:\mid{x}−\mathrm{1}\mid\:−\mathrm{2}\mid\:=\:\mid\:{x}−\mathrm{3}\:\mid\: \\ $$

Answered by bobhans last updated on 18/Dec/20

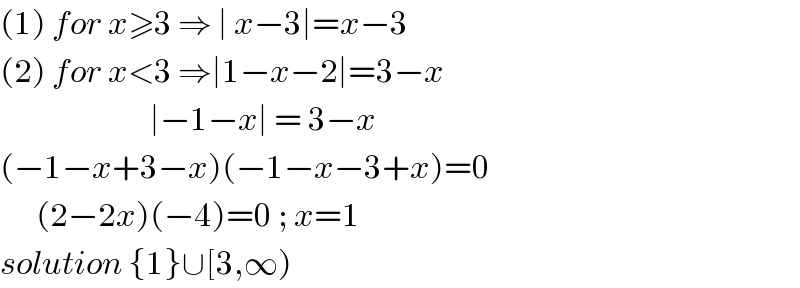
(1) for x≥3 ⇒ ∣ x−3∣=x−3 (2) for x<3 ⇒∣1−x−2∣=3−x ∣−1−x∣ = 3−x (−1−x+3−x)(−1−x−3+x)=0 (2−2x)(−4)=0 ; x=1 solution {1}∪[3,∞)

$$\left(\mathrm{1}\right)\:{for}\:{x}\geqslant\mathrm{3}\:\Rightarrow\:\mid\:{x}−\mathrm{3}\mid={x}−\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\:{for}\:{x}<\mathrm{3}\:\Rightarrow\mid\mathrm{1}−{x}−\mathrm{2}\mid=\mathrm{3}−{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid−\mathrm{1}−{x}\mid\:=\:\mathrm{3}−{x} \\ $$$$\left(−\mathrm{1}−{x}+\mathrm{3}−{x}\right)\left(−\mathrm{1}−{x}−\mathrm{3}+{x}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left(\mathrm{2}−\mathrm{2}{x}\right)\left(−\mathrm{4}\right)=\mathrm{0}\:;\:{x}=\mathrm{1} \\ $$$${solution}\:\left\{\mathrm{1}\right\}\cup\left[\mathrm{3},\infty\right) \\ $$

Answered by mathmax by abdo last updated on 18/Dec/20

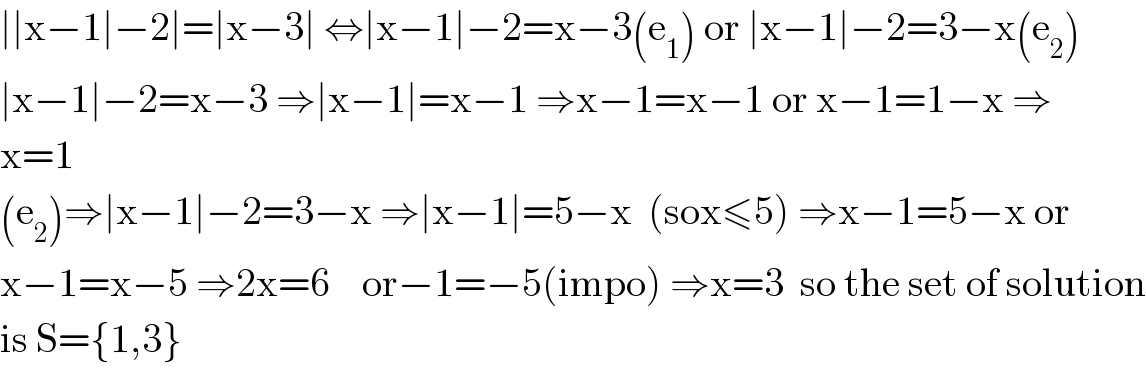
∣∣x−1∣−2∣=∣x−3∣ ⇔∣x−1∣−2=x−3(e_1 ) or ∣x−1∣−2=3−x(e_2 ) ∣x−1∣−2=x−3 ⇒∣x−1∣=x−1 ⇒x−1=x−1 or x−1=1−x ⇒ x=1 (e_2 )⇒∣x−1∣−2=3−x ⇒∣x−1∣=5−x (sox≤5) ⇒x−1=5−x or x−1=x−5 ⇒2x=6 or−1=−5(impo) ⇒x=3 so the set of solution is S={1,3}

$$\mid\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{2}\mid=\mid\mathrm{x}−\mathrm{3}\mid\:\Leftrightarrow\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{2}=\mathrm{x}−\mathrm{3}\left(\mathrm{e}_{\mathrm{1}} \right)\:\mathrm{or}\:\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{2}=\mathrm{3}−\mathrm{x}\left(\mathrm{e}_{\mathrm{2}} \right) \\ $$$$\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{2}=\mathrm{x}−\mathrm{3}\:\Rightarrow\mid\mathrm{x}−\mathrm{1}\mid=\mathrm{x}−\mathrm{1}\:\Rightarrow\mathrm{x}−\mathrm{1}=\mathrm{x}−\mathrm{1}\:\mathrm{or}\:\mathrm{x}−\mathrm{1}=\mathrm{1}−\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{x}=\mathrm{1} \\ $$$$\left(\mathrm{e}_{\mathrm{2}} \right)\Rightarrow\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{2}=\mathrm{3}−\mathrm{x}\:\Rightarrow\mid\mathrm{x}−\mathrm{1}\mid=\mathrm{5}−\mathrm{x}\:\:\left(\mathrm{sox}\leqslant\mathrm{5}\right)\:\Rightarrow\mathrm{x}−\mathrm{1}=\mathrm{5}−\mathrm{x}\:\mathrm{or} \\ $$$$\mathrm{x}−\mathrm{1}=\mathrm{x}−\mathrm{5}\:\Rightarrow\mathrm{2x}=\mathrm{6}\:\:\:\:\mathrm{or}−\mathrm{1}=−\mathrm{5}\left(\mathrm{impo}\right)\:\Rightarrow\mathrm{x}=\mathrm{3}\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{solution} \\ $$$$\mathrm{is}\:\mathrm{S}=\left\{\mathrm{1},\mathrm{3}\right\} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply