Menu Close

solve-x-1-y-1-x-y-x-e-2x-

Tinku Tara 0 Comments
Pin




Question Number 57415 by Abdo msup. last updated on 03/Apr/19
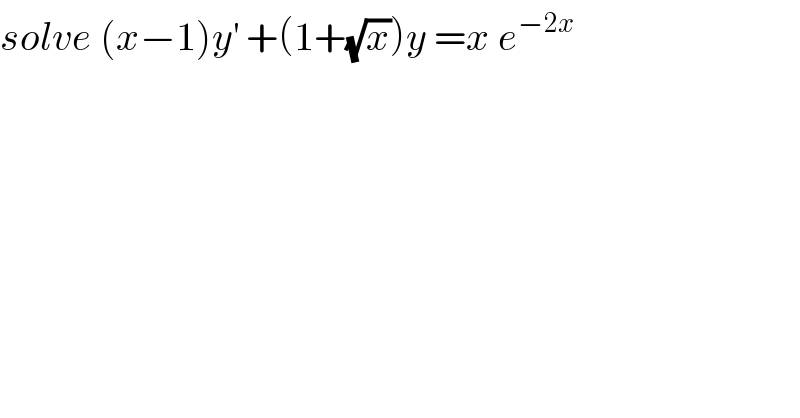
solve (x−1)y^′ +(1+(√x))y =x e^(−2x)
$${solve}\:\left({x}−\mathrm{1}\right){y}^{'} \:+\left(\mathrm{1}+\sqrt{{x}}\right){y}\:={x}\:{e}^{−\mathrm{2}{x}} \\ $$
Commented by maxmathsup by imad last updated on 12/Apr/19
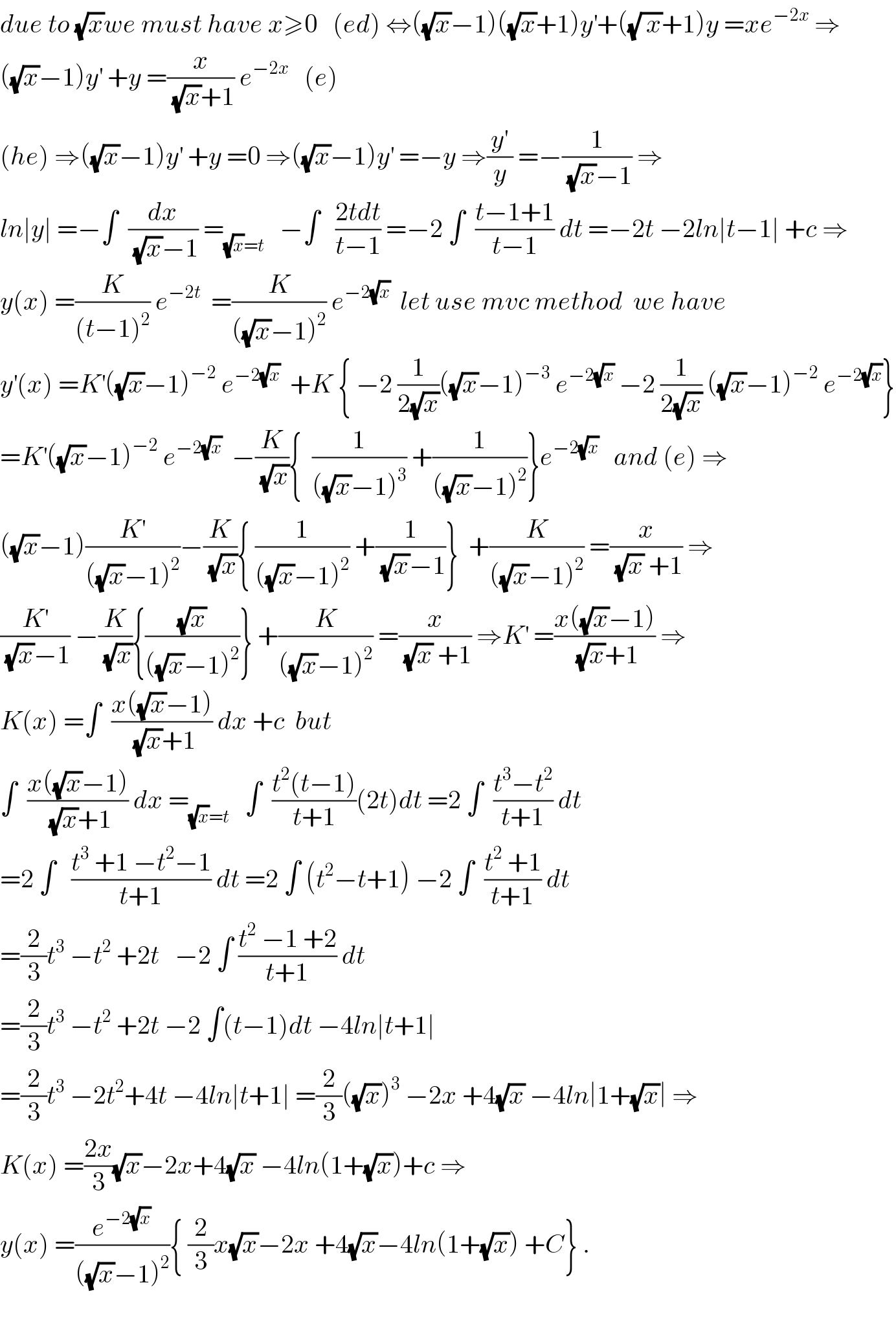
due to (√x)we must have x≥0 (ed) ⇔((√x)−1)((√x)+1)y^′ +((√( x))+1)y =xe^(−2x) ⇒ ((√x)−1)y^′ +y =(x/( (√x)+1)) e^(−2x) (e) (he) ⇒((√x)−1)y^′ +y =0 ⇒((√x)−1)y^′ =−y ⇒(y^′ /y) =−(1/( (√x)−1)) ⇒ ln∣y∣ =−∫ (dx/( (√x)−1)) =_((√x)=t) −∫ ((2tdt)/(t−1)) =−2 ∫ ((t−1+1)/(t−1)) dt =−2t −2ln∣t−1∣ +c ⇒ y(x) =(K/((t−1)^2 )) e^(−2t) =(K/(((√x)−1)^2 )) e^(−2(√x)) let use mvc method we have y^′ (x) =K^′ ((√x)−1)^(−2) e^(−2(√x)) +K { −2 (1/(2(√x)))((√x)−1)^(−3) e^(−2(√x)) −2 (1/(2(√x))) ((√x)−1)^(−2) e^(−2(√x)) } =K^′ ((√x)−1)^(−2) e^(−2(√x)) −(K/( (√x))){ (1/(((√x)−1)^3 )) +(1/(((√x)−1)^2 ))}e^(−2(√x)) and (e) ⇒ ((√x)−1)(K^′ /(((√x)−1)^2 ))−(K/( (√x))){ (1/(((√x)−1)^2 )) +(1/( (√x)−1))} +(K/(((√x)−1)^2 )) =(x/( (√x) +1)) ⇒ (K^′ /( (√x)−1)) −(K/( (√x))){((√x)/(((√x)−1)^2 ))} +(K/(((√x)−1)^2 )) =(x/( (√x) +1)) ⇒K^′ =((x((√x)−1))/( (√x)+1)) ⇒ K(x) =∫ ((x((√x)−1))/( (√x)+1)) dx +c but ∫ ((x((√x)−1))/( (√x)+1)) dx =_((√x)=t) ∫ ((t^2 (t−1))/(t+1))(2t)dt =2 ∫ ((t^3 −t^2 )/(t+1)) dt =2 ∫ ((t^3 +1 −t^2 −1)/(t+1)) dt =2 ∫ (t^2 −t+1) −2 ∫ ((t^2 +1)/(t+1)) dt =(2/3)t^3 −t^2 +2t −2 ∫ ((t^2 −1 +2)/(t+1)) dt =(2/3)t^3 −t^2 +2t −2 ∫(t−1)dt −4ln∣t+1∣ =(2/3)t^3 −2t^2 +4t −4ln∣t+1∣ =(2/3)((√x))^3 −2x +4(√x) −4ln∣1+(√x)∣ ⇒ K(x) =((2x)/3)(√x)−2x+4(√x) −4ln(1+(√x))+c ⇒ y(x) =(e^(−2(√x)) /(((√x)−1)^2 )){ (2/3)x(√x)−2x +4(√x)−4ln(1+(√x)) +C} .
$${due}\:{to}\:\sqrt{{x}}{we}\:{must}\:{have}\:{x}\geqslant\mathrm{0}\:\:\:\left({ed}\right)\:\Leftrightarrow\left(\sqrt{{x}}−\mathrm{1}\right)\left(\sqrt{{x}}+\mathrm{1}\right){y}^{'} +\left(\sqrt{\:{x}}+\mathrm{1}\right){y}\:={xe}^{−\mathrm{2}{x}} \:\Rightarrow \\ $$$$\left(\sqrt{{x}}−\mathrm{1}\right){y}^{'} \:+{y}\:=\frac{{x}}{\:\sqrt{{x}}+\mathrm{1}}\:{e}^{−\mathrm{2}{x}} \:\:\:\left({e}\right) \\ $$$$\left({he}\right)\:\Rightarrow\left(\sqrt{{x}}−\mathrm{1}\right){y}^{'} \:+{y}\:=\mathrm{0}\:\Rightarrow\left(\sqrt{{x}}−\mathrm{1}\right){y}^{'} \:=−{y}\:\Rightarrow\frac{{y}^{'} }{{y}}\:=−\frac{\mathrm{1}}{\:\sqrt{{x}}−\mathrm{1}}\:\Rightarrow \\ $$$${ln}\mid{y}\mid\:=−\int\:\:\frac{{dx}}{\:\sqrt{{x}}−\mathrm{1}}\:=_{\sqrt{{x}}={t}} \:\:\:−\int\:\:\:\frac{\mathrm{2}{tdt}}{{t}−\mathrm{1}}\:=−\mathrm{2}\:\int\:\:\frac{{t}−\mathrm{1}+\mathrm{1}}{{t}−\mathrm{1}}\:{dt}\:=−\mathrm{2}{t}\:−\mathrm{2}{ln}\mid{t}−\mathrm{1}\mid\:+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\frac{{K}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:{e}^{−\mathrm{2}{t}} \:\:=\frac{{K}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:{e}^{−\mathrm{2}\sqrt{{x}}} \:\:{let}\:{use}\:{mvc}\:{method}\:\:{we}\:{have} \\ $$$${y}^{'} \left({x}\right)\:={K}^{'} \left(\sqrt{{x}}−\mathrm{1}\right)^{−\mathrm{2}} \:{e}^{−\mathrm{2}\sqrt{{x}}} \:\:+{K}\:\left\{\:−\mathrm{2}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\left(\sqrt{{x}}−\mathrm{1}\right)^{−\mathrm{3}} \:{e}^{−\mathrm{2}\sqrt{{x}}} \:−\mathrm{2}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\:\left(\sqrt{{x}}−\mathrm{1}\right)^{−\mathrm{2}} \:{e}^{−\mathrm{2}\sqrt{{x}}} \right\} \\ $$$$={K}^{'} \left(\sqrt{{x}}−\mathrm{1}\right)^{−\mathrm{2}} \:{e}^{−\mathrm{2}\sqrt{{x}}} \:\:−\frac{{K}}{\:\sqrt{{x}}}\left\{\:\:\frac{\mathrm{1}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\right\}{e}^{−\mathrm{2}\sqrt{{x}}} \:\:\:{and}\:\left({e}\right)\:\Rightarrow \\ $$$$\left(\sqrt{{x}}−\mathrm{1}\right)\frac{{K}^{'} }{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{{K}}{\:\sqrt{{x}}}\left\{\:\frac{\mathrm{1}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\:\sqrt{{x}}−\mathrm{1}}\right\}\:\:+\frac{{K}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{{x}}{\:\sqrt{{x}}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{K}^{'} }{\:\sqrt{{x}}−\mathrm{1}}\:−\frac{{K}}{\:\sqrt{{x}}}\left\{\frac{\sqrt{{x}}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\right\}\:+\frac{{K}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{{x}}{\:\sqrt{{x}}\:+\mathrm{1}}\:\Rightarrow{K}^{'} \:=\frac{{x}\left(\sqrt{{x}}−\mathrm{1}\right)}{\:\sqrt{{x}}+\mathrm{1}}\:\Rightarrow \\ $$$${K}\left({x}\right)\:=\int\:\:\frac{{x}\left(\sqrt{{x}}−\mathrm{1}\right)}{\:\sqrt{{x}}+\mathrm{1}}\:{dx}\:+{c}\:\:{but} \\ $$$$\int\:\:\frac{{x}\left(\sqrt{{x}}−\mathrm{1}\right)}{\:\sqrt{{x}}+\mathrm{1}}\:{dx}\:=_{\sqrt{{x}}={t}} \:\:\:\int\:\:\frac{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}{{t}+\mathrm{1}}\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{3}} −{t}^{\mathrm{2}} }{{t}+\mathrm{1}}\:{dt} \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{1}\:−{t}^{\mathrm{2}} −\mathrm{1}}{{t}+\mathrm{1}}\:{dt}\:=\mathrm{2}\:\int\:\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\:−\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}+\mathrm{1}}\:{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} \:−{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:\:\:−\mathrm{2}\:\int\:\frac{{t}^{\mathrm{2}} \:−\mathrm{1}\:+\mathrm{2}}{{t}+\mathrm{1}}\:{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} \:−{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:−\mathrm{2}\:\int\left({t}−\mathrm{1}\right){dt}\:−\mathrm{4}{ln}\mid{t}+\mathrm{1}\mid \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} \:−\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}{t}\:−\mathrm{4}{ln}\mid{t}+\mathrm{1}\mid\:=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{{x}}\right)^{\mathrm{3}} \:−\mathrm{2}{x}\:+\mathrm{4}\sqrt{{x}}\:−\mathrm{4}{ln}\mid\mathrm{1}+\sqrt{{x}}\mid\:\Rightarrow \\ $$$${K}\left({x}\right)\:=\frac{\mathrm{2}{x}}{\mathrm{3}}\sqrt{{x}}−\mathrm{2}{x}+\mathrm{4}\sqrt{{x}}\:−\mathrm{4}{ln}\left(\mathrm{1}+\sqrt{{x}}\right)+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\frac{{e}^{−\mathrm{2}\sqrt{{x}}} }{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\left\{\:\frac{\mathrm{2}}{\mathrm{3}}{x}\sqrt{{x}}−\mathrm{2}{x}\:+\mathrm{4}\sqrt{{x}}−\mathrm{4}{ln}\left(\mathrm{1}+\sqrt{{x}}\right)\:+{C}\right\}\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *