Menu Close

solve-x-1-y-x-2-y-x-2-e-2x-with-y-3-1-

Tinku Tara 0 Comments
Pin




Question Number 57820 by maxmathsup by imad last updated on 12/Apr/19
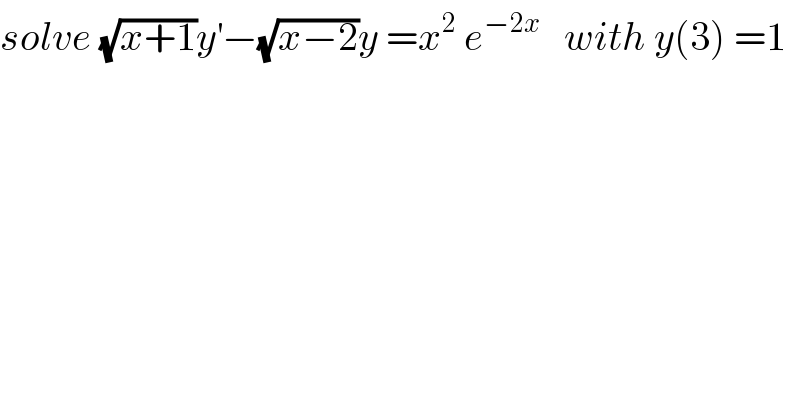
solve (√(x+1))y^′ −(√(x−2))y =x^2 e^(−2x) with y(3) =1
$${solve}\:\sqrt{{x}+\mathrm{1}}{y}^{'} −\sqrt{{x}−\mathrm{2}}{y}\:={x}^{\mathrm{2}} \:{e}^{−\mathrm{2}{x}} \:\:\:{with}\:{y}\left(\mathrm{3}\right)\:=\mathrm{1} \\ $$
Commented by maxmathsup by imad last updated on 14/Apr/19
(he) ⇒(√(x+1))y^′ −(√(x−2))y =0 ⇒(√(x+1))y^′ =(√(x−2))y ⇒(y^′ /y) =((√(x−2))/( (√(x+1)))) ⇒ ln∣y∣ = ∫ (√((x−2)/(x+1)))dx +c changement (√((x−2)/(x+1)))=t give((x−2)/(x+1)) =t^2 ⇒ x−2 =t^2 x +t^2 ⇒(1−t^2 )x =t^2 +2 ⇒x =((t^2 +2)/(1−t^2 )) ⇒(dx/dt) =((2t(1−t^2 )−(t^2 +2)(−2t))/((1−t^2 )^2 )) =((2t−2t^3 +2t^3 +4t)/((1−t^2 )^2 )) =((6t)/((1−t^2 )^2 )) ⇒∫(√((x−2)/(x+1)))dx =∫ ((6t^2 )/((1−t^2 )^2 )) dt we have ∫ (t^2 /((t^2 −1)^2 )) dt =∫ t (t/((t^2 −1)^2 )) dt by parts u =t and v^′ =(t/((t^2 −1)^2 )) ⇒∫ (t^2 /((t^2 −1)^2 )) dt =−(1/(2(t^2 −1))) t −∫ −(1/(2(t^2 −1))) dt =−(t/(2(t^2 −1))) +(1/2) ∫ ((1/(t−1)) −(1/(t+1)))dt =−(t/(2(t^2 −1))) +(1/2)ln∣((t−1)/(t+1))∣ ⇒ ∫(√((x−2)/(x+1))) dx =−((√((x−2)/(x+1)))/(2(((x−2)/(x+1))−1))) +(1/2)ln∣(((√((x−2)/(x+1)))−1)/( (√((x−2)/(x+1)))+1))∣ =−((√(x−2))/(2(√(x+1)))) (1/((((−3)/(x+1))))) +(1/2)ln∣(((√(x−2))−(√(x+1)))/( (√(x−2)) +(√(x+1))))∣ =(((√(x−2))(x+1))/(6(√(x+1)))) +(1/2)ln(....) =(((√(x−2))(√(x+1)))/6) +(1/2)ln∣(((√(x−2))−(√(x+1)))/( (√(x−2)) +(√(x+1))))∣ ⇒ y(x) = K (√(((√(x+1))−(√(x−2)))/( (√(x+1)) +(√(x−2)))))e^(((√(x−2))(√(x+1)))/6) after we use the mvc method... be continued...
$$\left({he}\right)\:\Rightarrow\sqrt{{x}+\mathrm{1}}{y}^{'} −\sqrt{{x}−\mathrm{2}}{y}\:=\mathrm{0}\:\Rightarrow\sqrt{{x}+\mathrm{1}}{y}^{'} =\sqrt{{x}−\mathrm{2}}{y}\:\Rightarrow\frac{{y}^{'} }{{y}}\:=\frac{\sqrt{{x}−\mathrm{2}}}{\:\sqrt{{x}+\mathrm{1}}}\:\Rightarrow \\ $$$${ln}\mid{y}\mid\:=\:\int\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}{dx}\:+{c}\:\:\:\:\:\:{changement}\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}={t}\:{give}\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}−\mathrm{2}\:={t}^{\mathrm{2}} {x}\:+{t}^{\mathrm{2}} \:\Rightarrow\left(\mathrm{1}−{t}^{\mathrm{2}} \right){x}\:={t}^{\mathrm{2}} \:+\mathrm{2}\:\Rightarrow{x}\:=\frac{{t}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow\frac{{dx}}{{dt}}\:=\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)−\left({t}^{\mathrm{2}} +\mathrm{2}\right)\left(−\mathrm{2}{t}\right)}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{4}{t}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{6}{t}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\int\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}{dx}\:=\int\:\frac{\mathrm{6}{t}^{\mathrm{2}} }{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dt} \\ $$$${we}\:{have}\:\int\:\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:=\int\:\:{t}\:\frac{{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:\:{by}\:{parts}\:{u}\:={t}\:{and}\:{v}^{'} \:=\frac{{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int\:\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}\:{t}\:−\int\:−\frac{\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}\:{dt} \\ $$$$=−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\left(\frac{\mathrm{1}}{{t}−\mathrm{1}}\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}\:=−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:\Rightarrow \\ $$$$\int\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}\:{dx}\:=−\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}}{\mathrm{2}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}−\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}+\mathrm{1}}\mid \\ $$$$=−\frac{\sqrt{{x}−\mathrm{2}}}{\mathrm{2}\sqrt{{x}+\mathrm{1}}}\:\frac{\mathrm{1}}{\left(\frac{−\mathrm{3}}{{x}+\mathrm{1}}\right)}\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\sqrt{{x}−\mathrm{2}}−\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}−\mathrm{2}}\:+\sqrt{{x}+\mathrm{1}}}\mid\:=\frac{\sqrt{{x}−\mathrm{2}}\left({x}+\mathrm{1}\right)}{\mathrm{6}\sqrt{{x}+\mathrm{1}}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(….\right) \\ $$$$=\frac{\sqrt{{x}−\mathrm{2}}\sqrt{{x}+\mathrm{1}}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\sqrt{{x}−\mathrm{2}}−\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}−\mathrm{2}}\:+\sqrt{{x}+\mathrm{1}}}\mid\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\:{K}\:\sqrt{\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{2}}}{\:\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}−\mathrm{2}}}}{e}^{\frac{\sqrt{{x}−\mathrm{2}}\sqrt{{x}+\mathrm{1}}}{\mathrm{6}}} \:\:\:\:{after}\:{we}\:{use}\:{the}\:{mvc}\:{method}… \\ $$$${be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *