Question Number 58963 by Tony Lin last updated on 02/May/19
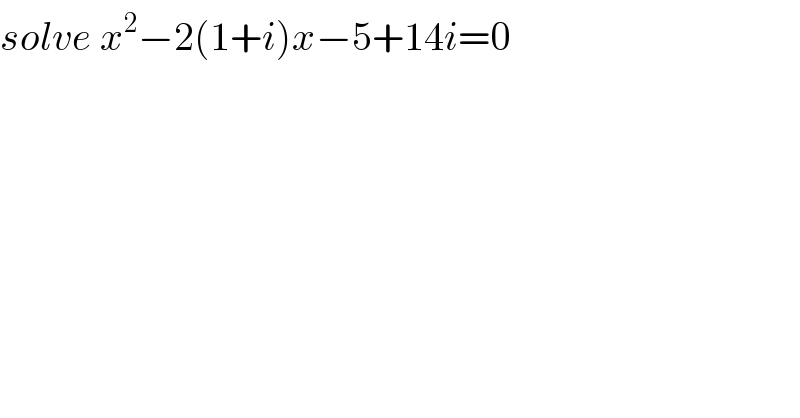
$${solve}\:{x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+{i}\right){x}−\mathrm{5}+\mathrm{14}{i}=\mathrm{0} \\ $$
Answered by tanmay last updated on 02/May/19
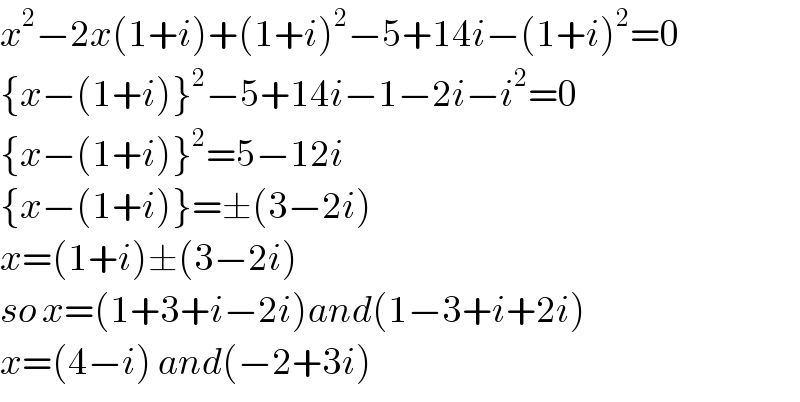
$${x}^{\mathrm{2}} −\mathrm{2}{x}\left(\mathrm{1}+{i}\right)+\left(\mathrm{1}+{i}\right)^{\mathrm{2}} −\mathrm{5}+\mathrm{14}{i}−\left(\mathrm{1}+{i}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left\{{x}−\left(\mathrm{1}+{i}\right)\right\}^{\mathrm{2}} −\mathrm{5}+\mathrm{14}{i}−\mathrm{1}−\mathrm{2}{i}−{i}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left\{{x}−\left(\mathrm{1}+{i}\right)\right\}^{\mathrm{2}} =\mathrm{5}−\mathrm{12}{i} \\ $$$$\left\{{x}−\left(\mathrm{1}+{i}\right)\right\}=\pm\left(\mathrm{3}−\mathrm{2}{i}\right) \\ $$$${x}=\left(\mathrm{1}+{i}\right)\pm\left(\mathrm{3}−\mathrm{2}{i}\right) \\ $$$${so}\:{x}=\left(\mathrm{1}+\mathrm{3}+{i}−\mathrm{2}{i}\right){and}\left(\mathrm{1}−\mathrm{3}+{i}+\mathrm{2}{i}\right) \\ $$$${x}=\left(\mathrm{4}−{i}\right)\:{and}\left(−\mathrm{2}+\mathrm{3}{i}\right) \\ $$
Commented by Tony Lin last updated on 02/May/19

$${thanks},{sir} \\ $$
Commented by tanmay last updated on 02/May/19

$${most}\:{welcome} \\ $$
