Question Number 114592 by Aziztisffola last updated on 19/Sep/20
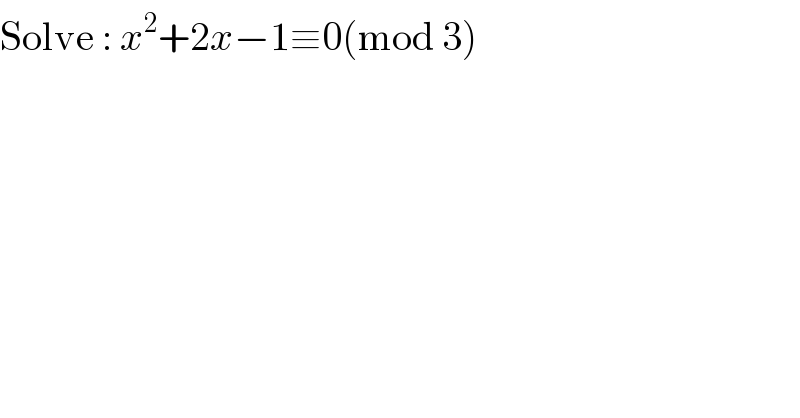
Answered by MJS_new last updated on 19/Sep/20
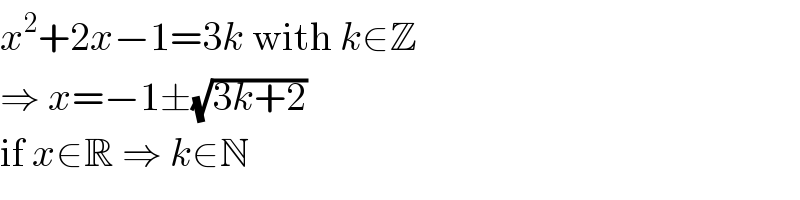
Commented by Aziztisffola last updated on 19/Sep/20
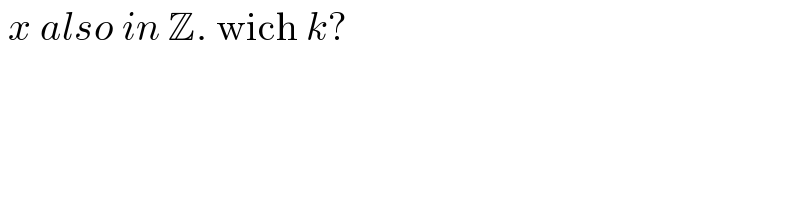
Commented by Aziztisffola last updated on 19/Sep/20
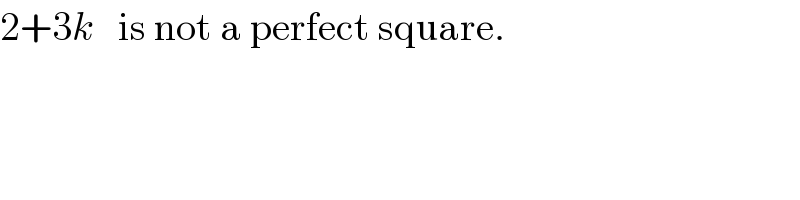
Commented by MJS_new last updated on 19/Sep/20

Commented by Aziztisffola last updated on 19/Sep/20
Answered by floor(10²Eta[1]) last updated on 19/Sep/20
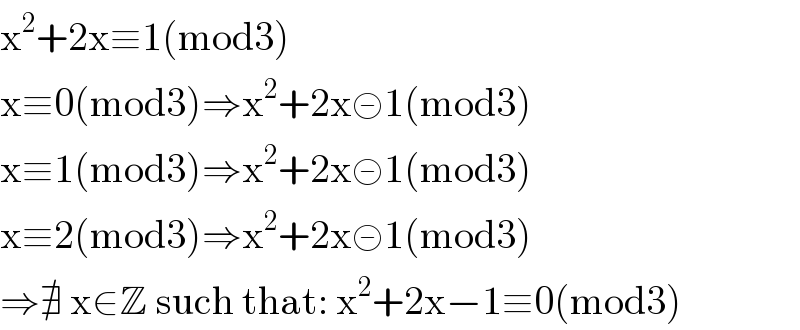
Commented by Aziztisffola last updated on 19/Sep/20
![yes sir that′s it. x^2 +2x−1≡0(mod3) ⇔(x+1)^2 ≡2[3] ⇔(x+1)^2 =2+3k /k∈Z and 2+3k≠ n^2 for n in Z. then no solution.](https://www.tinkutara.com/question/Q114610.png)
Answered by 1549442205PVT last updated on 20/Sep/20

