Question Number 88160 by john santu last updated on 08/Apr/20
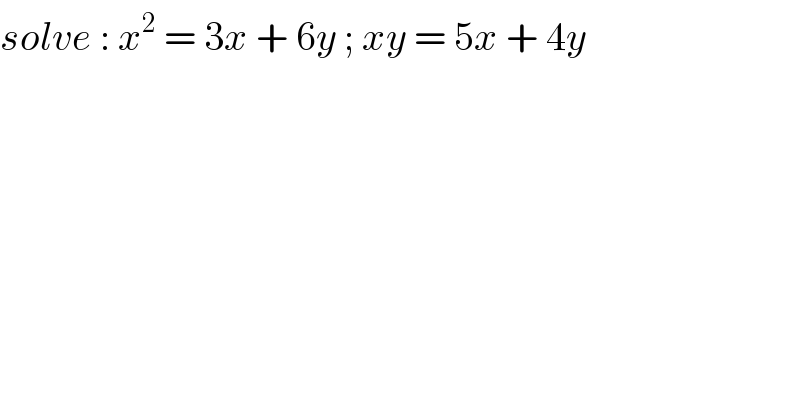
$${solve}\::\:{x}^{\mathrm{2}} \:=\:\mathrm{3}{x}\:+\:\mathrm{6}{y}\:;\:{xy}\:=\:\mathrm{5}{x}\:+\:\mathrm{4}{y} \\ $$
Commented by john santu last updated on 08/Apr/20

$${y}\:=\:\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}}{\mathrm{6}}\:\:;\:{y}\left({x}−\mathrm{4}\right)\:=\:\mathrm{5}{x} \\ $$$$\Rightarrow\:\frac{\left({x}^{\mathrm{2}} −\mathrm{3}{x}\right)\left({x}−\mathrm{4}\right)}{\mathrm{6}}\:=\:\mathrm{5}{x} \\ $$$${x}^{\mathrm{3}} −\mathrm{7}{x}^{\mathrm{2}} +\mathrm{12}{x}\:=\:\mathrm{30}{x} \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}\right)\:=\:\mathrm{0} \\ $$$${x}\:\left({x}−\mathrm{9}\right)\left({x}+\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{0}\:\wedge\:{y}\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{9}\:\wedge\:{y}=\:\mathrm{9} \\ $$$${x}\:=\:−\mathrm{2}\:\wedge\:{y}\:=\:\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by ajfour last updated on 08/Apr/20

$${x}^{\mathrm{2}} −\mathrm{3}{x}=\frac{\mathrm{6}×\mathrm{5}{x}}{{x}−\mathrm{4}}\:\: \\ $$$${x}\left\{\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)−\mathrm{30}\right\}=\mathrm{0} \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{2},\:\mathrm{0},\:\mathrm{9},\: \\ $$$${y}=\frac{\mathrm{5}{x}}{{x}−\mathrm{4}}\:. \\ $$
Answered by $@ty@m123 last updated on 08/Apr/20

$$\mathrm{3}{x}+\mathrm{6}{y}={x}^{\mathrm{2}} \:\:…\left(\mathrm{1}\right) \\ $$$$\mathrm{5}{x}+\mathrm{4}{y}={xy}\:…\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)×\mathrm{2}\:−\left(\mathrm{2}\right)×\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{6}{x}+\:\:\:\:\:\:\:\:\mathrm{12}{y}=\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\:_{\left(−\right)} \mathrm{15}{x}+\:\:_{\left(−\right)} \mathrm{12}{y}=\:_{\left(−\right)} \mathrm{3}{xy} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:−\mathrm{9}{x}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{xy} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${y}=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}}{\mathrm{3}{x}} \\ $$$${y}=\frac{\mathrm{2}}{\mathrm{3}}{x}+\mathrm{3}\:…\left(\mathrm{3}\right) \\ $$$$\therefore\:{from}\:\left(\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{6}\left(\frac{\mathrm{2}}{\mathrm{3}}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}=\mathrm{0} \\ $$$$\left({x}−\mathrm{9}\right)\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{2},\mathrm{9} \\ $$$$\therefore\:{from}\:\left(\mathrm{3}\right), \\ $$$${y}=\frac{\mathrm{5}}{\mathrm{3}},\mathrm{9} \\ $$
Commented by jagoll last updated on 08/Apr/20

$$\mathrm{x}\:=\:\mathrm{0}\:?\:\mathrm{not}\:\mathrm{solution}? \\ $$
Commented by jagoll last updated on 08/Apr/20

$$\mathrm{i}\:\mathrm{think}\:\mathrm{x}\:=\:\mathrm{0}\:\mathrm{is}\:\mathrm{solution}. \\ $$
