Question Number 21355 by Tinkutara last updated on 21/Sep/17
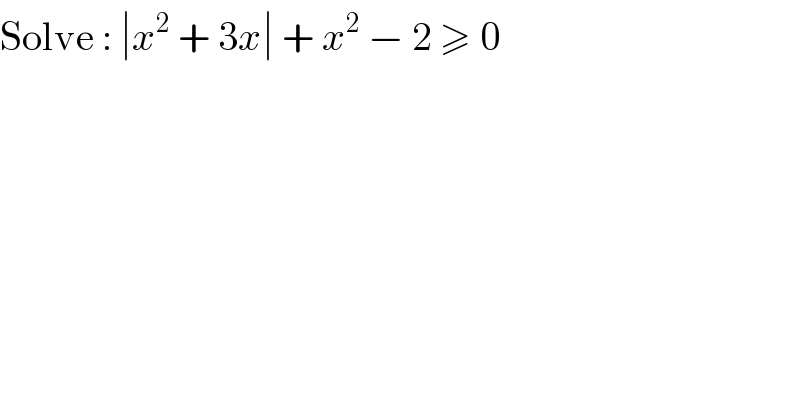
$$\mathrm{Solve}\::\:\mid{x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\mid\:+\:{x}^{\mathrm{2}} \:−\:\mathrm{2}\:\geqslant\:\mathrm{0} \\ $$
Answered by mrW1 last updated on 22/Sep/17
![∣x^2 +3x∣≥2−x^2 1. x^2 +3x≥0 { ((x^2 +3x≥0 ⇒x(x+3)≥0)),((x^2 +3x≥2−x^2 ⇒2x^2 +3x−2≥0 ⇒(2x−1)(x+2)≥0)) :} ⇒ { ((x≥0 or x≤−3)),((x≥(1/2) or x≤−2)) :} ⇒x≥(1/2) or x≤−3 2. x^2 +3x≤0 { ((x^2 +3x≤0 ⇒x(x+3)≤0 ⇒−3≤x≤0)),((−(x^2 +3x)≥2−x^2 ⇒−3x≥2 ⇒x≤−(2/3))) :} ⇒−3≤x≤−(2/3) ⇒x∈(−∞,−(2/3)] or [(1/2),+∞)](https://www.tinkutara.com/question/Q21381.png)
$$\mid\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\mid\geqslant\mathrm{2}−\mathrm{x}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{1}.\:\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\geqslant\mathrm{0}\: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\geqslant\mathrm{0}\:\Rightarrow\mathrm{x}\left(\mathrm{x}+\mathrm{3}\right)\geqslant\mathrm{0}}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\geqslant\mathrm{2}−\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}\geqslant\mathrm{0}\:\Rightarrow\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\geqslant\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}\geqslant\mathrm{0}\:\mathrm{or}\:\mathrm{x}\leqslant−\mathrm{3}}\\{\mathrm{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{or}\:\mathrm{x}\leqslant−\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\mathrm{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{or}\:\mathrm{x}\leqslant−\mathrm{3} \\ $$$$ \\ $$$$\mathrm{2}.\:\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\leqslant\mathrm{0}\: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\leqslant\mathrm{0}\:\Rightarrow\mathrm{x}\left(\mathrm{x}+\mathrm{3}\right)\leqslant\mathrm{0}\:\Rightarrow−\mathrm{3}\leqslant\mathrm{x}\leqslant\mathrm{0}}\\{−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\right)\geqslant\mathrm{2}−\mathrm{x}^{\mathrm{2}} \:\Rightarrow−\mathrm{3x}\geqslant\mathrm{2}\:\Rightarrow\mathrm{x}\leqslant−\frac{\mathrm{2}}{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow−\mathrm{3}\leqslant\mathrm{x}\leqslant−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{x}\in\left(−\infty,−\frac{\mathrm{2}}{\mathrm{3}}\right]\:\mathrm{or}\:\left[\frac{\mathrm{1}}{\mathrm{2}},+\infty\right) \\ $$
Commented by Tinkutara last updated on 22/Sep/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
