Question Number 172031 by Mikenice last updated on 23/Jun/22
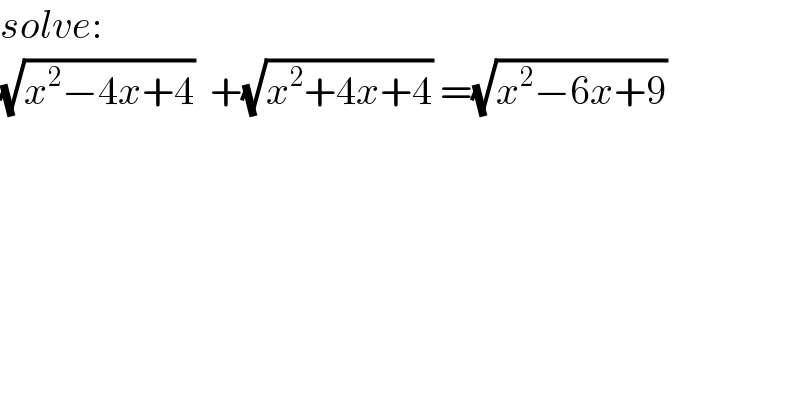
$${solve}: \\ $$$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}\:\:+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}\:=\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}} \\ $$
Answered by puissant last updated on 23/Jun/22
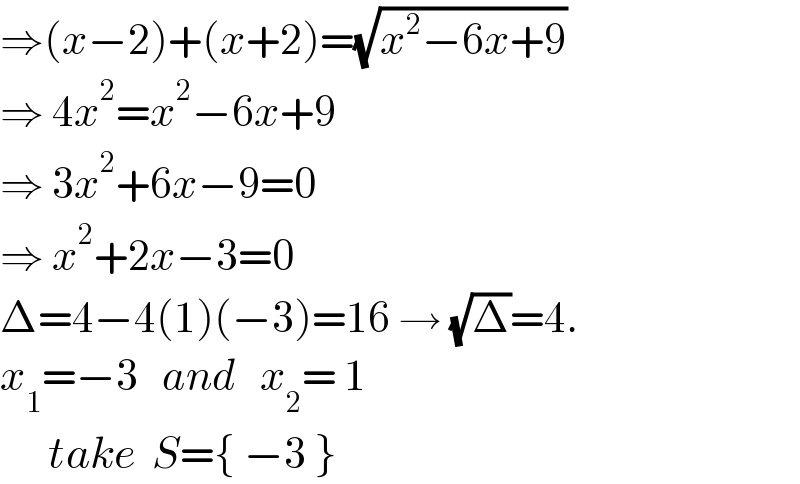
$$\Rightarrow\left({x}−\mathrm{2}\right)+\left({x}+\mathrm{2}\right)=\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}} \\ $$$$\Rightarrow\:\mathrm{4}{x}^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9} \\ $$$$\Rightarrow\:\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{9}=\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\Delta=\mathrm{4}−\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{3}\right)=\mathrm{16}\:\rightarrow\:\sqrt{\Delta}=\mathrm{4}. \\ $$$${x}_{\mathrm{1}} =−\mathrm{3}\:\:\:{and}\:\:\:{x}_{\mathrm{2}} =\:\mathrm{1} \\ $$$$\:\:\:\:\:\:{take}\:\:{S}=\left\{\:−\mathrm{3}\:\right\} \\ $$
Commented by Mikenice last updated on 23/Jun/22

$${thanks}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Jun/22

$${x}=\mathrm{1}\:{is}\:{not}\:{valid}. \\ $$
Answered by Rasheed.Sindhi last updated on 23/Jun/22
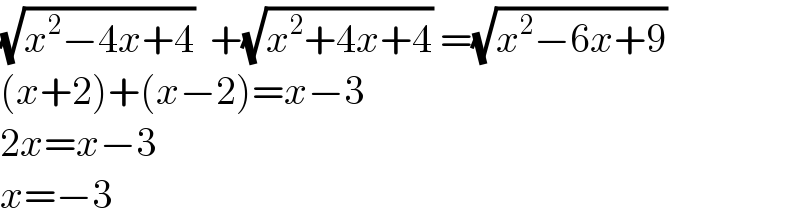
$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}\:\:+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}\:=\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}} \\ $$$$\left({x}+\mathrm{2}\right)+\left({x}−\mathrm{2}\right)={x}−\mathrm{3} \\ $$$$\mathrm{2}{x}={x}−\mathrm{3} \\ $$$${x}=−\mathrm{3} \\ $$
Answered by kapoorshah last updated on 23/Jun/22
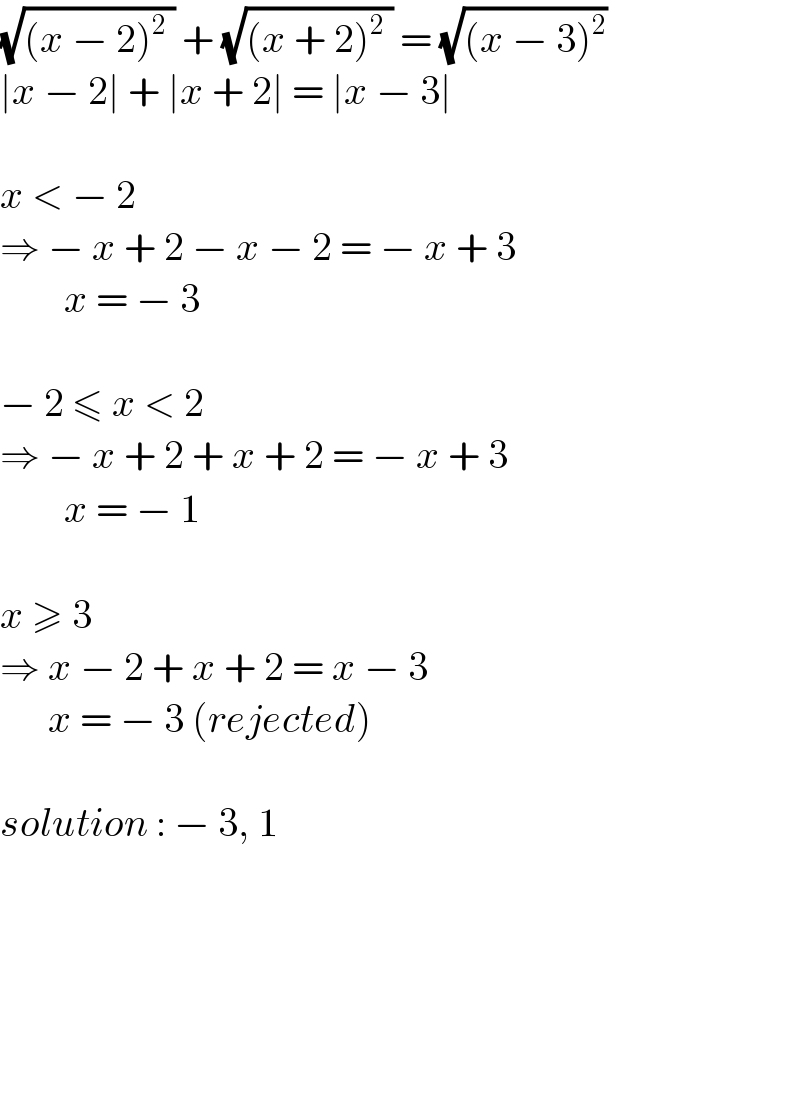
$$\sqrt{\left({x}\:−\:\mathrm{2}\right)^{\mathrm{2}} \:}\:+\:\sqrt{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:}\:=\:\sqrt{\left({x}\:−\:\mathrm{3}\right)^{\mathrm{2}} }\: \\ $$$$\mid{x}\:−\:\mathrm{2}\mid\:+\:\mid{x}\:+\:\mathrm{2}\mid\:=\:\mid{x}\:−\:\mathrm{3}\mid \\ $$$$ \\ $$$${x}\:<\:−\:\mathrm{2}\: \\ $$$$\Rightarrow\:−\:{x}\:+\:\mathrm{2}\:−\:{x}\:−\:\mathrm{2}\:=\:−\:{x}\:+\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:{x}\:=\:−\:\mathrm{3} \\ $$$$ \\ $$$$−\:\mathrm{2}\:\leqslant\:{x}\:<\:\mathrm{2}\: \\ $$$$\Rightarrow\:−\:{x}\:+\:\mathrm{2}\:+\:{x}\:+\:\mathrm{2}\:=\:−\:{x}\:+\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:{x}\:=\:−\:\mathrm{1} \\ $$$$ \\ $$$${x}\:\geqslant\:\mathrm{3}\: \\ $$$$\Rightarrow\:{x}\:−\:\mathrm{2}\:+\:{x}\:+\:\mathrm{2}\:=\:{x}\:−\:\mathrm{3} \\ $$$$\:\:\:\:\:\:{x}\:=\:−\:\mathrm{3}\:\left({rejected}\right) \\ $$$$ \\ $$$${solution}\::\:−\:\mathrm{3},\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
