Question Number 24662 by NECx last updated on 24/Nov/17
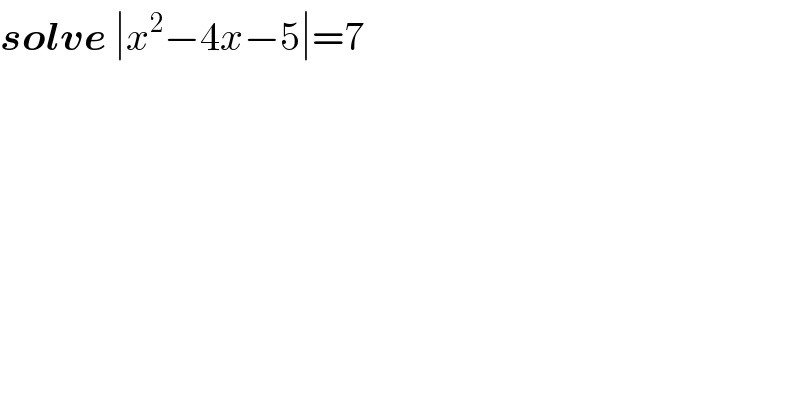
$$\boldsymbol{{solve}}\:\mid{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}\mid=\mathrm{7} \\ $$$$ \\ $$
Answered by mrW1 last updated on 24/Nov/17
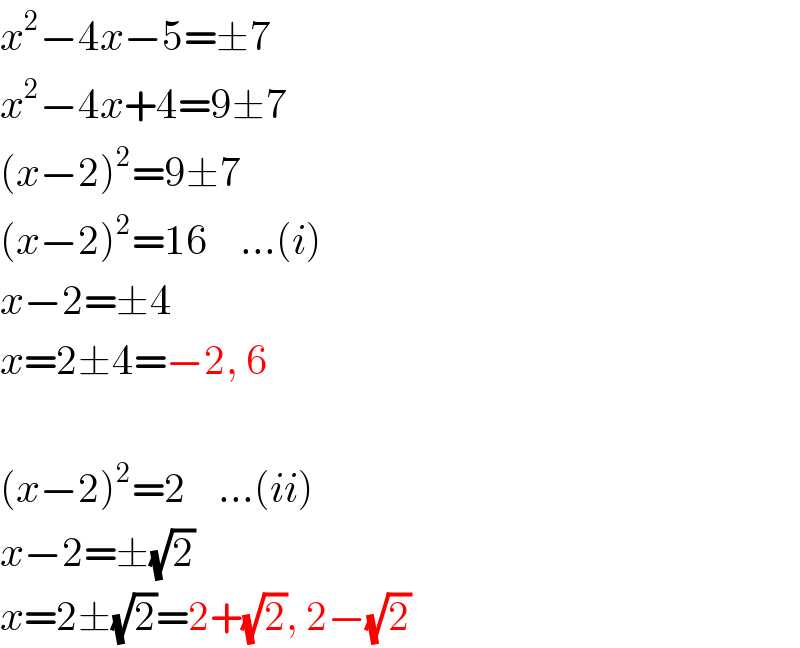
$${x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}=\pm\mathrm{7} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}=\mathrm{9}\pm\mathrm{7} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{9}\pm\mathrm{7} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{16}\:\:\:\:…\left({i}\right) \\ $$$${x}−\mathrm{2}=\pm\mathrm{4} \\ $$$${x}=\mathrm{2}\pm\mathrm{4}=−\mathrm{2},\:\mathrm{6} \\ $$$$ \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{2}\:\:\:\:…\left({ii}\right) \\ $$$${x}−\mathrm{2}=\pm\sqrt{\mathrm{2}} \\ $$$${x}=\mathrm{2}\pm\sqrt{\mathrm{2}}=\mathrm{2}+\sqrt{\mathrm{2}},\:\mathrm{2}−\sqrt{\mathrm{2}} \\ $$
Commented by NECx last updated on 24/Nov/17
$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$
Commented by NECx last updated on 24/Nov/17

$${can}\:{the}\:{answers}\:{from}\:{an}\:{absolute} \\ $$$${value}\:{also}\:{be}\:{represented}\:{in} \\ $$$${intervals},{if}\:{so}\:{please}\:{how}\:{can}\:{the} \\ $$$${answer}\:{be}\:{represented}. \\ $$
Commented by Joel578 last updated on 24/Nov/17

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{couldn}'\mathrm{t} \\ $$
