Question Number 172006 by Mikenice last updated on 23/Jun/22
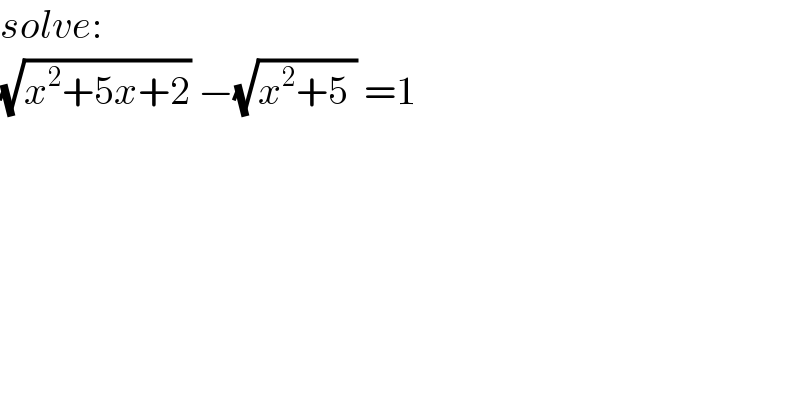
$${solve}: \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}}\:−\sqrt{{x}^{\mathrm{2}} +\mathrm{5}\:}\:=\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 24/Jun/22
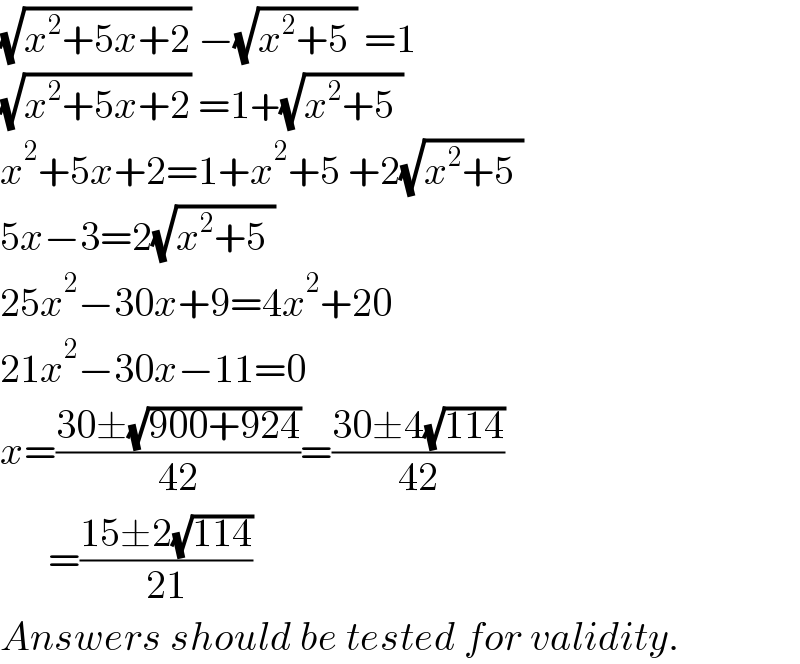
$$\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}}\:−\sqrt{{x}^{\mathrm{2}} +\mathrm{5}\:}\:=\mathrm{1} \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}}\:=\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{5}\:}\: \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}=\mathrm{1}+{x}^{\mathrm{2}} +\mathrm{5}\:+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{5}\:}\: \\ $$$$\mathrm{5}{x}−\mathrm{3}=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{5}\:}\: \\ $$$$\mathrm{25}{x}^{\mathrm{2}} −\mathrm{30}{x}+\mathrm{9}=\mathrm{4}{x}^{\mathrm{2}} +\mathrm{20} \\ $$$$\mathrm{21}{x}^{\mathrm{2}} −\mathrm{30}{x}−\mathrm{11}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{30}\pm\sqrt{\mathrm{900}+\mathrm{924}}}{\mathrm{42}}=\frac{\mathrm{30}\pm\mathrm{4}\sqrt{\mathrm{114}}}{\mathrm{42}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{15}\pm\mathrm{2}\sqrt{\mathrm{114}}}{\mathrm{21}} \\ $$$${Answers}\:{should}\:{be}\:{tested}\:{for}\:{validity}. \\ $$
