Question Number 173051 by mr W last updated on 05/Jul/22
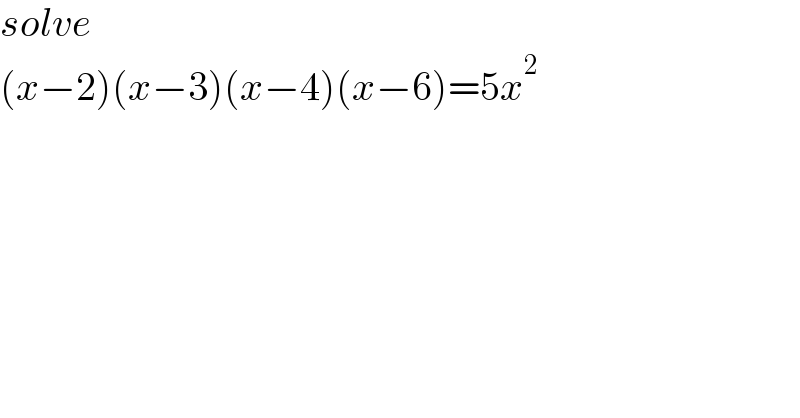
$${solve} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{6}\right)=\mathrm{5}{x}^{\mathrm{2}} \\ $$
Answered by dragan91 last updated on 06/Jul/22
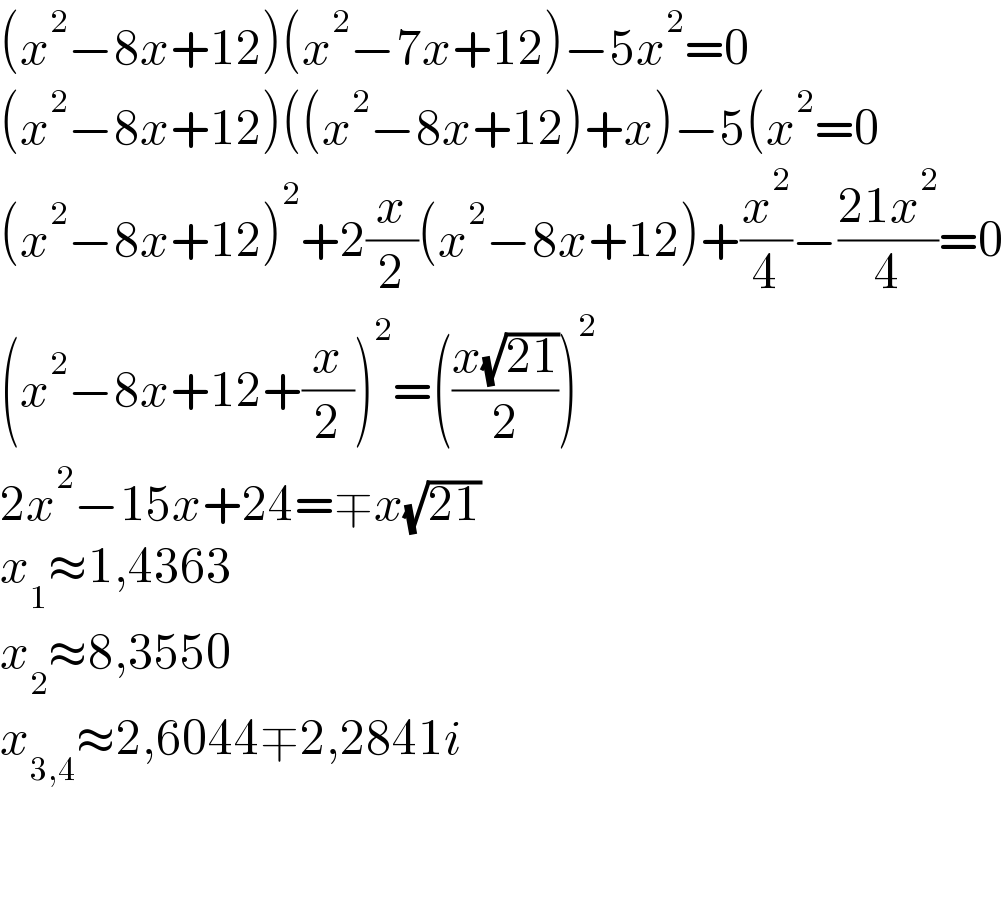
$$\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\right)\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}\right)−\mathrm{5}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\right)\left(\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\right)+{x}\right)−\mathrm{5}\left({x}^{\mathrm{2}} =\mathrm{0}\right. \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\right)^{\mathrm{2}} +\mathrm{2}\frac{{x}}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{21}{x}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}+\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{x}\sqrt{\mathrm{21}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{15}{x}+\mathrm{24}=\mp{x}\sqrt{\mathrm{21}} \\ $$$${x}_{\mathrm{1}} \approx\mathrm{1},\mathrm{4363} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{8},\mathrm{3550} \\ $$$${x}_{\mathrm{3},\mathrm{4}} \approx\mathrm{2},\mathrm{6044}\mp\mathrm{2},\mathrm{2841}{i} \\ $$$$ \\ $$$$ \\ $$
Answered by MJS_new last updated on 06/Jul/22
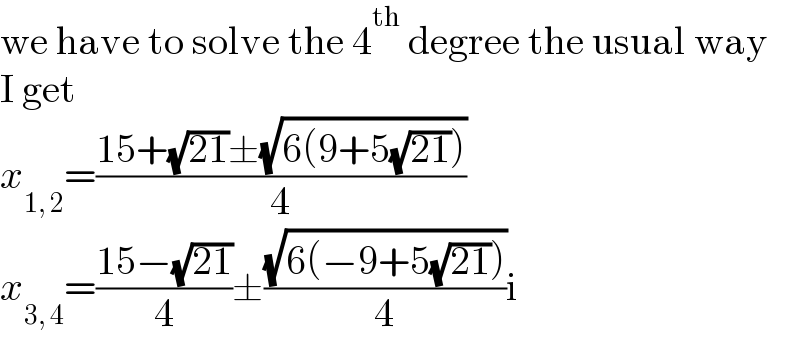
$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{way} \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\frac{\mathrm{15}+\sqrt{\mathrm{21}}\pm\sqrt{\mathrm{6}\left(\mathrm{9}+\mathrm{5}\sqrt{\mathrm{21}}\right)}}{\mathrm{4}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\frac{\mathrm{15}−\sqrt{\mathrm{21}}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{6}\left(−\mathrm{9}+\mathrm{5}\sqrt{\mathrm{21}}\right)}}{\mathrm{4}}\mathrm{i} \\ $$
Commented by mr W last updated on 06/Jul/22

$${thanks}\:{sirs}! \\ $$
Commented by dragan91 last updated on 06/Jul/22
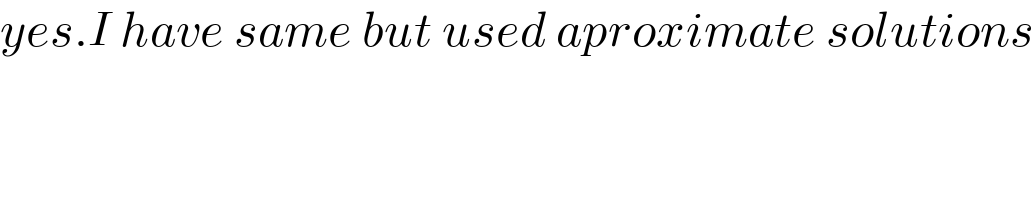
$${yes}.{I}\:{have}\:{same}\:{but}\:{used}\:{aproximate}\:{solutions} \\ $$
Commented by mr W last updated on 06/Jul/22
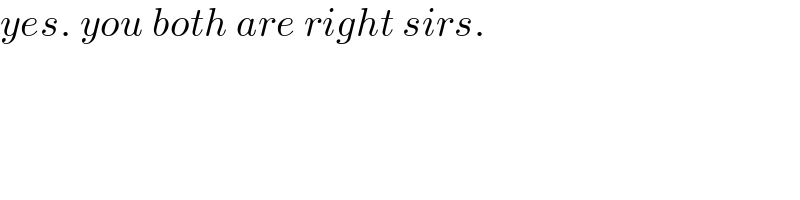
$${yes}.\:{you}\:{both}\:{are}\:{right}\:{sirs}. \\ $$
Answered by mr W last updated on 06/Jul/22
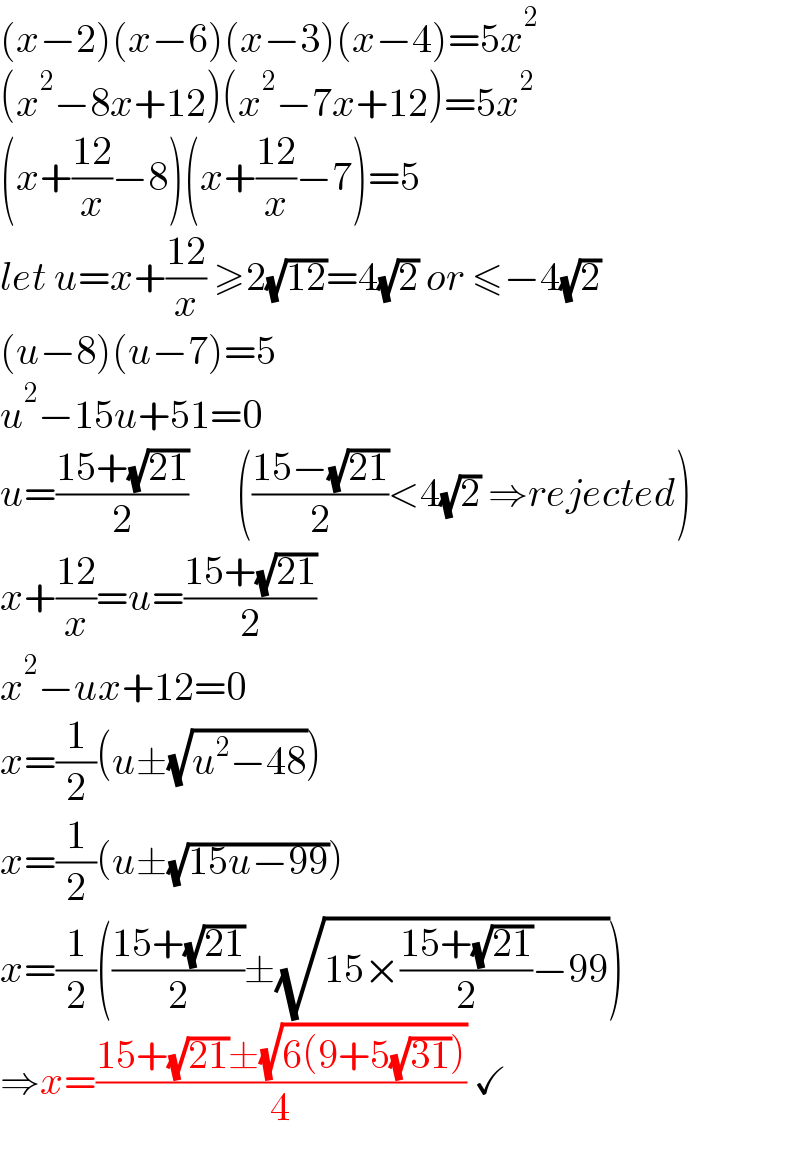
$$\left({x}−\mathrm{2}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)=\mathrm{5}{x}^{\mathrm{2}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{12}\right)\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}\right)=\mathrm{5}{x}^{\mathrm{2}} \\ $$$$\left({x}+\frac{\mathrm{12}}{{x}}−\mathrm{8}\right)\left({x}+\frac{\mathrm{12}}{{x}}−\mathrm{7}\right)=\mathrm{5} \\ $$$${let}\:{u}={x}+\frac{\mathrm{12}}{{x}}\:\geqslant\mathrm{2}\sqrt{\mathrm{12}}=\mathrm{4}\sqrt{\mathrm{2}}\:{or}\:\leqslant−\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$\left({u}−\mathrm{8}\right)\left({u}−\mathrm{7}\right)=\mathrm{5} \\ $$$${u}^{\mathrm{2}} −\mathrm{15}{u}+\mathrm{51}=\mathrm{0} \\ $$$${u}=\frac{\mathrm{15}+\sqrt{\mathrm{21}}}{\mathrm{2}}\:\:\:\:\:\:\left(\frac{\mathrm{15}−\sqrt{\mathrm{21}}}{\mathrm{2}}<\mathrm{4}\sqrt{\mathrm{2}}\:\Rightarrow{rejected}\right) \\ $$$${x}+\frac{\mathrm{12}}{{x}}={u}=\frac{\mathrm{15}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{ux}+\mathrm{12}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left({u}\pm\sqrt{{u}^{\mathrm{2}} −\mathrm{48}}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left({u}\pm\sqrt{\mathrm{15}{u}−\mathrm{99}}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{15}+\sqrt{\mathrm{21}}}{\mathrm{2}}\pm\sqrt{\mathrm{15}×\frac{\mathrm{15}+\sqrt{\mathrm{21}}}{\mathrm{2}}−\mathrm{99}}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{15}+\sqrt{\mathrm{21}}\pm\sqrt{\mathrm{6}\left(\mathrm{9}+\mathrm{5}\sqrt{\mathrm{31}}\right)}}{\mathrm{4}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 06/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
