Question Number 158156 by mnjuly1970 last updated on 31/Oct/21
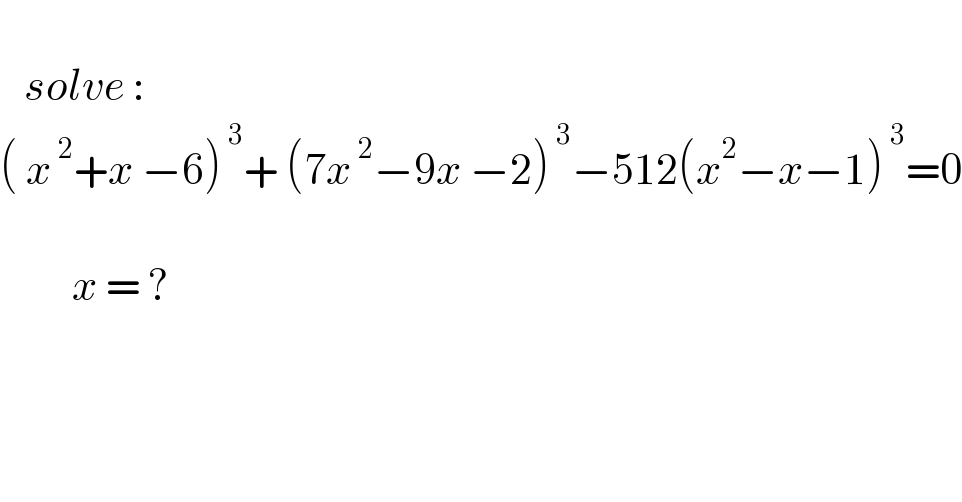
$$ \\ $$$$\:\:\:{solve}\:: \\ $$$$\left(\:{x}^{\:\mathrm{2}} +{x}\:−\mathrm{6}\right)^{\:\mathrm{3}} +\:\left(\mathrm{7}{x}^{\:\mathrm{2}} −\mathrm{9}{x}\:−\mathrm{2}\right)^{\:\mathrm{3}} −\mathrm{512}\left({x}^{\mathrm{2}} −{x}−\mathrm{1}\right)^{\:\mathrm{3}} =\mathrm{0} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:{x}\:=\:? \\ $$$$ \\ $$
Answered by som(math1967) last updated on 31/Oct/21
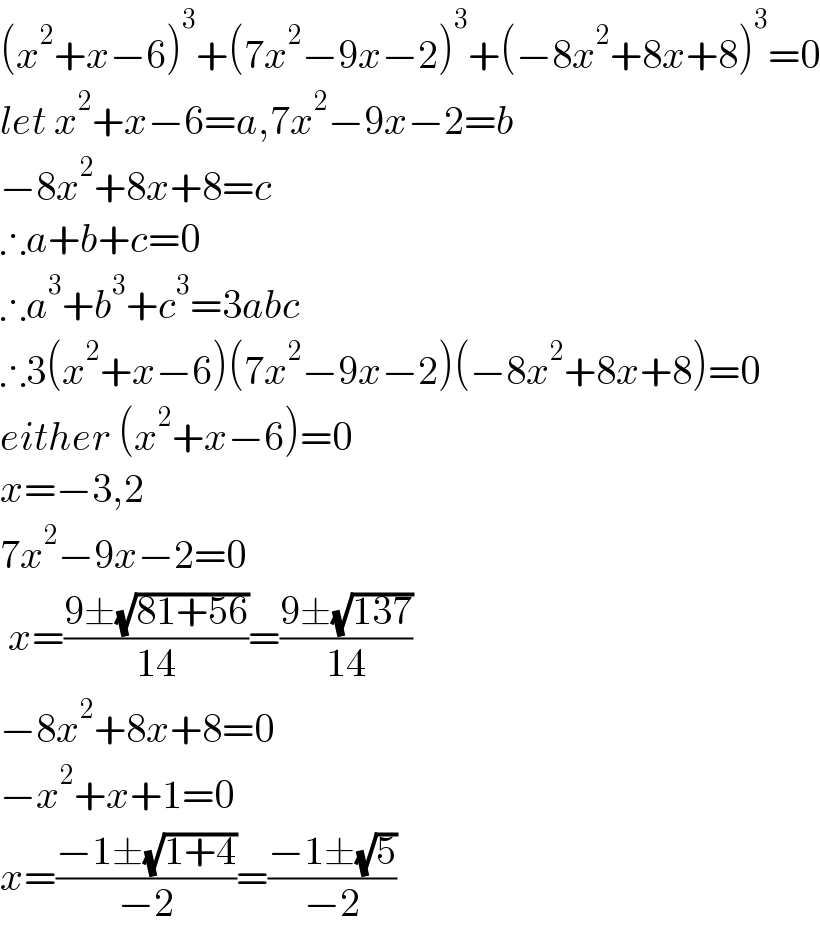
$$\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)^{\mathrm{3}} +\left(\mathrm{7}{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{2}\right)^{\mathrm{3}} +\left(−\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$${let}\:{x}^{\mathrm{2}} +{x}−\mathrm{6}={a},\mathrm{7}{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{2}={b} \\ $$$$−\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}={c} \\ $$$$\therefore{a}+{b}+{c}=\mathrm{0} \\ $$$$\therefore{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc} \\ $$$$\therefore\mathrm{3}\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)\left(\mathrm{7}{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{2}\right)\left(−\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}\right)=\mathrm{0} \\ $$$${either}\:\left({x}^{\mathrm{2}} +{x}−\mathrm{6}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{3},\mathrm{2} \\ $$$$\mathrm{7}{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\:{x}=\frac{\mathrm{9}\pm\sqrt{\mathrm{81}+\mathrm{56}}}{\mathrm{14}}=\frac{\mathrm{9}\pm\sqrt{\mathrm{137}}}{\mathrm{14}} \\ $$$$−\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}=\mathrm{0} \\ $$$$−{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{−\mathrm{2}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{−\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 31/Oct/21

$${grateful}\:{sir}… \\ $$
