Question Number 100327 by bobhans last updated on 26/Jun/20

$$\mathcal{S}\mathrm{olve}\:\mathrm{x}^{\mathrm{2}} \mathrm{y}''−\mathrm{3xy}'−\mathrm{5y}=\mathrm{0} \\ $$
Commented by bobhans last updated on 26/Jun/20
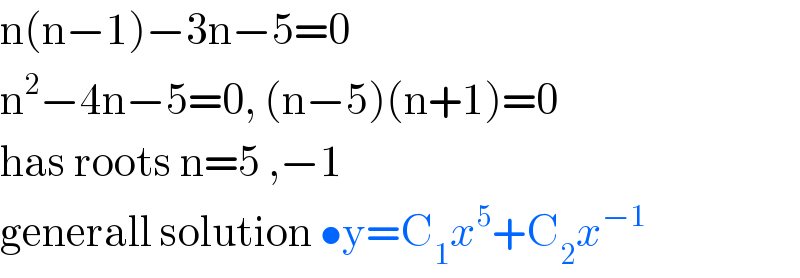
$$\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)−\mathrm{3n}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{n}^{\mathrm{2}} −\mathrm{4n}−\mathrm{5}=\mathrm{0},\:\left(\mathrm{n}−\mathrm{5}\right)\left(\mathrm{n}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{roots}\:\mathrm{n}=\mathrm{5}\:,−\mathrm{1} \\ $$$$\mathrm{generall}\:\mathrm{solution}\:\bullet\mathrm{y}=\mathrm{C}_{\mathrm{1}} {x}^{\mathrm{5}} +\mathrm{C}_{\mathrm{2}} {x}^{−\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 27/Jun/20
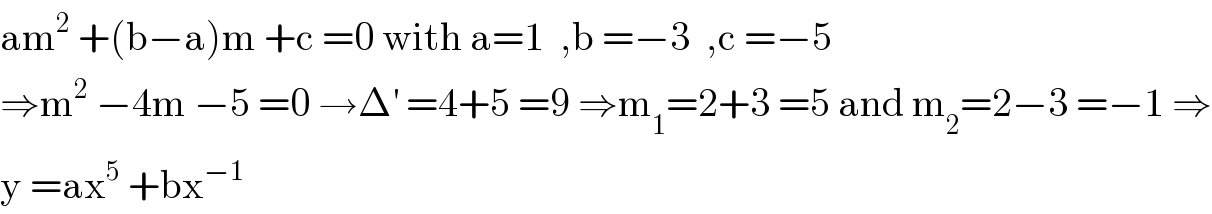
$$\mathrm{am}^{\mathrm{2}} \:+\left(\mathrm{b}−\mathrm{a}\right)\mathrm{m}\:+\mathrm{c}\:=\mathrm{0}\:\mathrm{with}\:\mathrm{a}=\mathrm{1}\:\:,\mathrm{b}\:=−\mathrm{3}\:\:,\mathrm{c}\:=−\mathrm{5} \\ $$$$\Rightarrow\mathrm{m}^{\mathrm{2}} \:−\mathrm{4m}\:−\mathrm{5}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{4}+\mathrm{5}\:=\mathrm{9}\:\Rightarrow\mathrm{m}_{\mathrm{1}} =\mathrm{2}+\mathrm{3}\:=\mathrm{5}\:\mathrm{and}\:\mathrm{m}_{\mathrm{2}} =\mathrm{2}−\mathrm{3}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{ax}^{\mathrm{5}} \:+\mathrm{bx}^{−\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 27/Jun/20
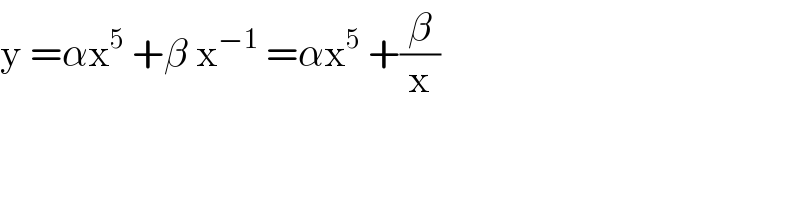
$$\mathrm{y}\:=\alpha\mathrm{x}^{\mathrm{5}} \:+\beta\:\mathrm{x}^{−\mathrm{1}} \:=\alpha\mathrm{x}^{\mathrm{5}} \:+\frac{\beta}{\mathrm{x}} \\ $$
