Question Number 90641 by Tony Lin last updated on 25/Apr/20
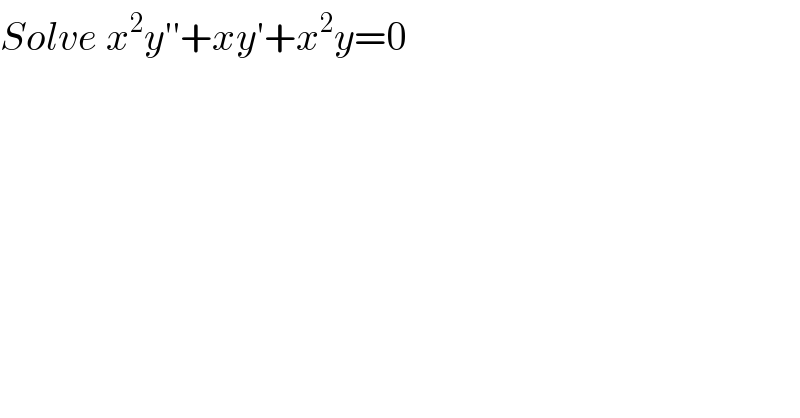
$${Solve}\:{x}^{\mathrm{2}} {y}''+{xy}'+{x}^{\mathrm{2}} {y}=\mathrm{0} \\ $$
Commented by jagoll last updated on 25/Apr/20

$${Euler}\:−\:{Cauchy}? \\ $$
Commented by Joel578 last updated on 25/Apr/20

$${nope}.\:\mathrm{It}\:\mathrm{is}\:\mathrm{Bessel}\:\mathrm{differential}\:\mathrm{equation} \\ $$$${x}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:{x}\:\frac{{dy}}{{dx}}\:+\:\left({x}^{\mathrm{2}} \:−\:\nu^{\mathrm{2}} \right){y}\left({x}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{General}\:\mathrm{solution}\:\mathrm{if}\:\nu\:=\:\mathrm{non}\:\mathrm{integer} \\ $$$${y}\left({x}\right)\:=\:{c}_{\mathrm{1}} {J}_{\nu} \left({x}\right)\:+\:{c}_{\mathrm{2}} {J}_{−\nu} \left({x}\right) \\ $$$$\mathrm{If}\:\nu\:=\:\mathrm{integer} \\ $$$${y}\left({x}\right)\:=\:{c}_{\mathrm{1}} {J}_{\nu} \left({x}\right)\:+\:{c}_{\mathrm{2}} {Y}_{\nu} \left({x}\right) \\ $$$$ \\ $$$${J}_{\nu} \left({x}\right)\::\:\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{m}} }{{m}!\:\left({m}+\nu\right)!}\:\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}{m}+\nu} \\ $$$${Y}_{\nu} \left({x}\right)\::\:\frac{\mathrm{cos}\:\left(\nu\pi\right){J}_{\nu} \left({x}\right)\:−\:{J}_{−\nu} \left({x}\right)}{\mathrm{sin}\:\left(\nu\pi\right)} \\ $$
Commented by Tony Lin last updated on 25/Apr/20

$${thanks}\:{sir} \\ $$
Commented by Joel578 last updated on 25/Apr/20
$${sorry}.\:{edit}\:{small}\:{typo} \\ $$
