Question Number 103411 by abdomsup last updated on 14/Jul/20
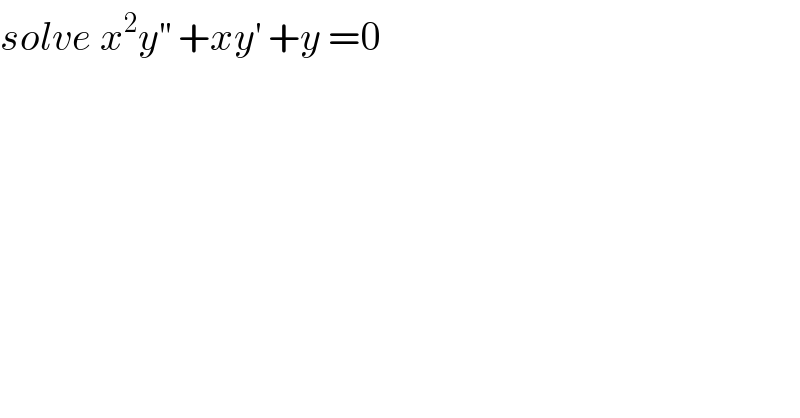
$${solve}\:{x}^{\mathrm{2}} {y}^{''} \:+{xy}^{'} \:+{y}\:=\mathrm{0} \\ $$
Answered by bemath last updated on 14/Jul/20
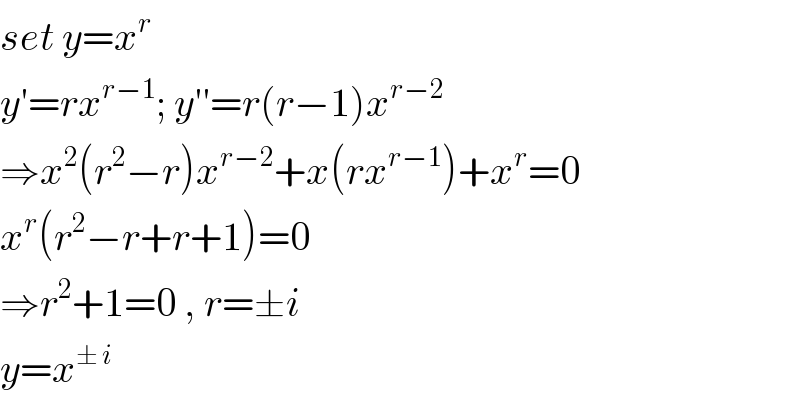
$${set}\:{y}={x}^{{r}} \\ $$$${y}'={rx}^{{r}−\mathrm{1}} ;\:{y}''={r}\left({r}−\mathrm{1}\right){x}^{{r}−\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left({r}^{\mathrm{2}} −{r}\right){x}^{{r}−\mathrm{2}} +{x}\left({rx}^{{r}−\mathrm{1}} \right)+{x}^{{r}} =\mathrm{0} \\ $$$${x}^{{r}} \left({r}^{\mathrm{2}} −{r}+{r}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:,\:{r}=\pm{i} \\ $$$${y}={x}^{\pm\:{i}} \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
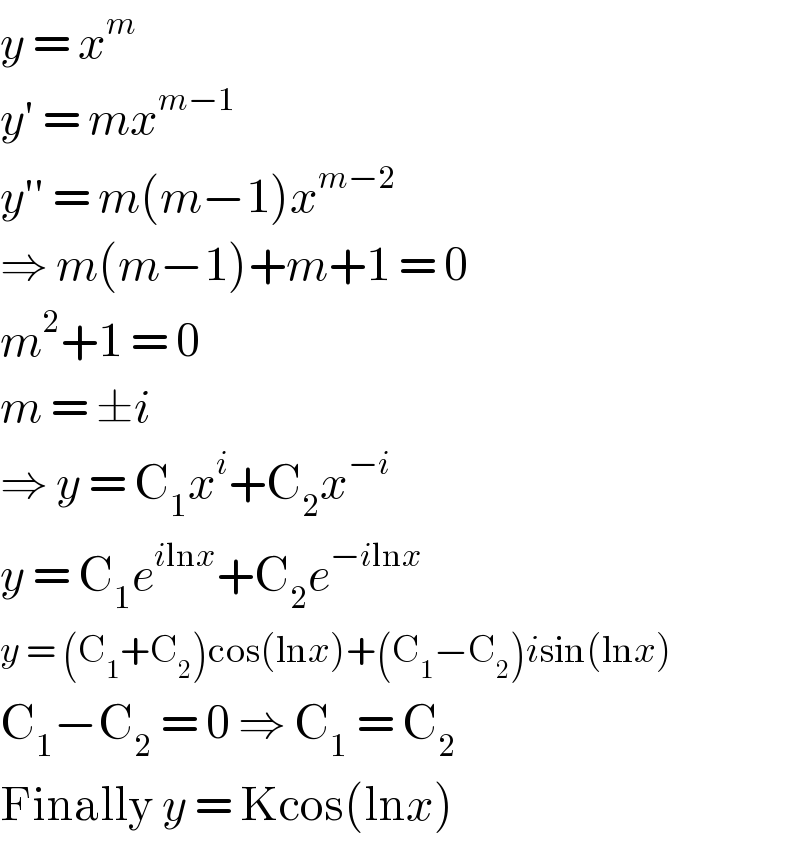
$${y}\:=\:{x}^{{m}} \\ $$$${y}'\:=\:{mx}^{{m}−\mathrm{1}} \\ $$$${y}''\:=\:{m}\left({m}−\mathrm{1}\right){x}^{{m}−\mathrm{2}} \\ $$$$\Rightarrow\:{m}\left({m}−\mathrm{1}\right)+{m}+\mathrm{1}\:=\:\mathrm{0} \\ $$$${m}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{0} \\ $$$${m}\:=\:\pm{i} \\ $$$$\Rightarrow\:{y}\:=\:\mathrm{C}_{\mathrm{1}} {x}^{{i}} +\mathrm{C}_{\mathrm{2}} {x}^{−{i}} \\ $$$${y}\:=\:\mathrm{C}_{\mathrm{1}} {e}^{{i}\mathrm{ln}{x}} +\mathrm{C}_{\mathrm{2}} {e}^{−{i}\mathrm{ln}{x}} \\ $$$${y}\:=\:\left(\mathrm{C}_{\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \right)\mathrm{cos}\left(\mathrm{ln}{x}\right)+\left(\mathrm{C}_{\mathrm{1}} −\mathrm{C}_{\mathrm{2}} \right){i}\mathrm{sin}\left(\mathrm{ln}{x}\right) \\ $$$$\mathrm{C}_{\mathrm{1}} −\mathrm{C}_{\mathrm{2}} \:=\:\mathrm{0}\:\Rightarrow\:\mathrm{C}_{\mathrm{1}} \:=\:\mathrm{C}_{\mathrm{2}} \\ $$$$\mathrm{Finally}\:{y}\:=\:\mathrm{Kcos}\left(\mathrm{ln}{x}\right) \\ $$
