solve-x-2-y-xy-y-0-on-0-put-x-e-t-

Question Number 65044 by mathmax by abdo last updated on 24/Jul/19

s o l v e x^{2} y^{^{″}} + {x y}^{^{'}} + y = 0 o n] 0, + \infty [(p u t x = e^{t})

Commented by mathmax by abdo last updated on 08/Aug/19

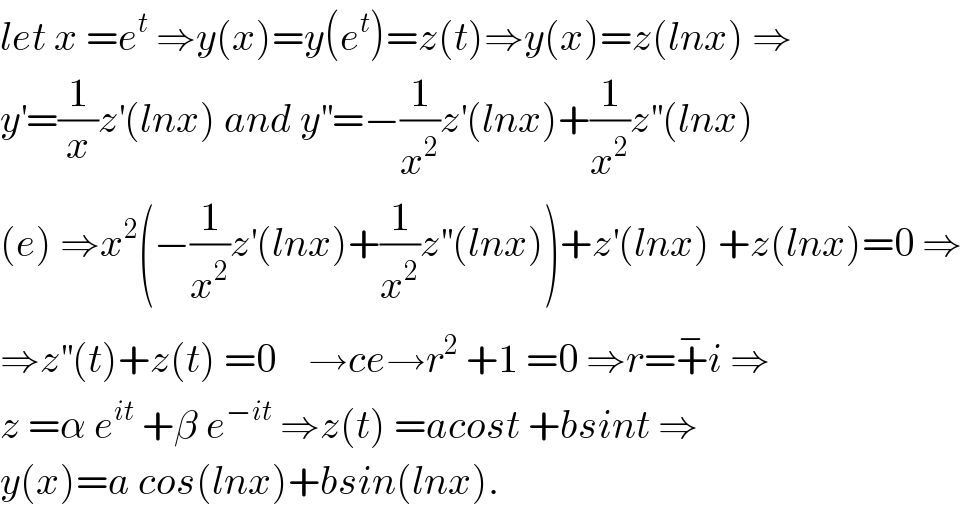
l e t x = e^{t} \Rightarrow y (x) = y (e^{t}) = z (t) \Rightarrow y (x) = z (l n x) \Rightarrow

y^{^{'}} = \frac{1}{x} z^{^{'}} (l n x) a n d y^{^{″}} = - \frac{1}{x^{2}} z^{^{'}} (l n x) + \frac{1}{x^{2}} z^{^{″}} (l n x)

(e) \Rightarrow x^{2} (- \frac{1}{x^{2}} z^{^{'}} (l n x) + \frac{1}{x^{2}} z^{^{″}} (l n x)) + z^{^{'}} (l n x) + z (l n x) = 0 \Rightarrow

\Rightarrow z^{^{″}} (t) + z (t) = 0 \to c e \to r^{2} + 1 = 0 \Rightarrow r = \bar{+} i \Rightarrow

z = α e^{i t} + β e^{- i t} \Rightarrow z (t) = a c o s t + b s i n t \Rightarrow

y (x) = a c o s (l n x) + b s i n (l n x) .