Question Number 156709 by aliyn last updated on 14/Oct/21
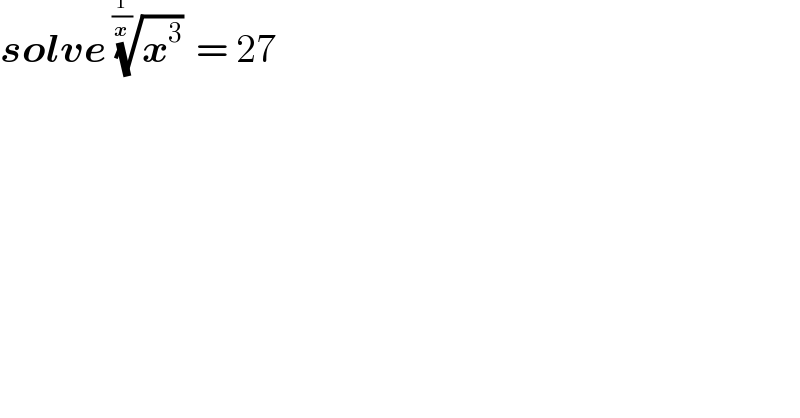
$$\boldsymbol{{solve}}\:\sqrt[{\frac{\mathrm{1}}{\boldsymbol{{x}}}}]{\boldsymbol{{x}}^{\mathrm{3}} }\:=\:\mathrm{27} \\ $$
Answered by mr W last updated on 14/Oct/21
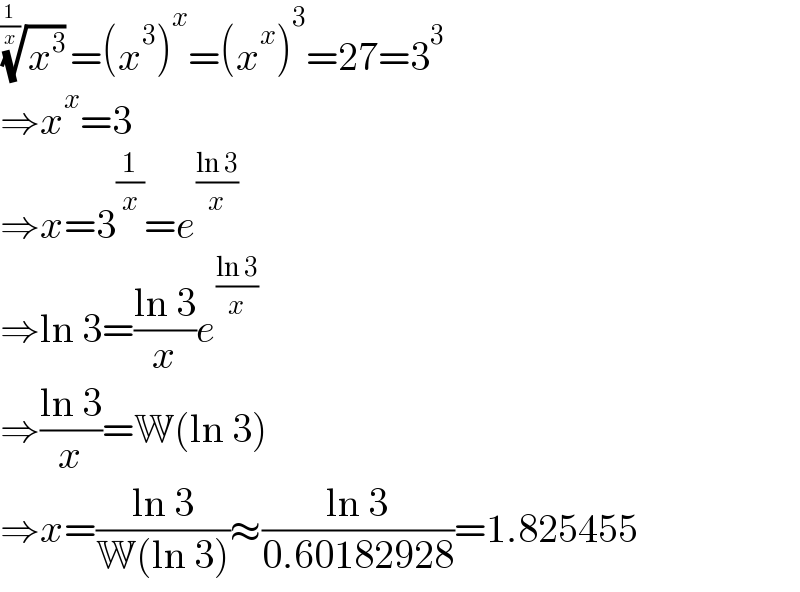
$$\sqrt[{\frac{\mathrm{1}}{{x}}}]{{x}^{\mathrm{3}} }=\left({x}^{\mathrm{3}} \right)^{{x}} =\left({x}^{{x}} \right)^{\mathrm{3}} =\mathrm{27}=\mathrm{3}^{\mathrm{3}} \\ $$$$\Rightarrow{x}^{{x}} =\mathrm{3} \\ $$$$\Rightarrow{x}=\mathrm{3}^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{ln}\:\mathrm{3}}{{x}}} \\ $$$$\Rightarrow\mathrm{ln}\:\mathrm{3}=\frac{\mathrm{ln}\:\mathrm{3}}{{x}}{e}^{\frac{\mathrm{ln}\:\mathrm{3}}{{x}}} \\ $$$$\Rightarrow\frac{\mathrm{ln}\:\mathrm{3}}{{x}}=\mathbb{W}\left(\mathrm{ln}\:\mathrm{3}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathbb{W}\left(\mathrm{ln}\:\mathrm{3}\right)}\approx\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{0}.\mathrm{60182928}}=\mathrm{1}.\mathrm{825455} \\ $$
Commented by tabata last updated on 14/Oct/21
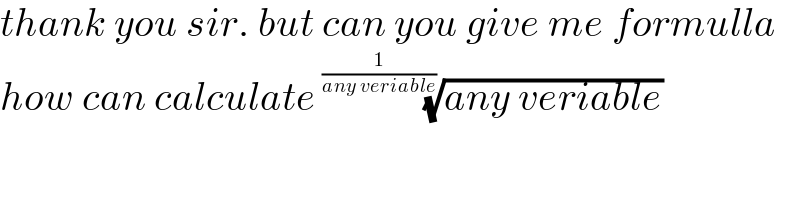
$${thank}\:{you}\:{sir}.\:{but}\:{can}\:{you}\:{give}\:{me}\:{formulla} \\ $$$${how}\:{can}\:{calculate}\:\sqrt[{\frac{\mathrm{1}}{{any}\:{veriable}}}]{{any}\:{veriable}} \\ $$
Commented by mr W last updated on 14/Oct/21
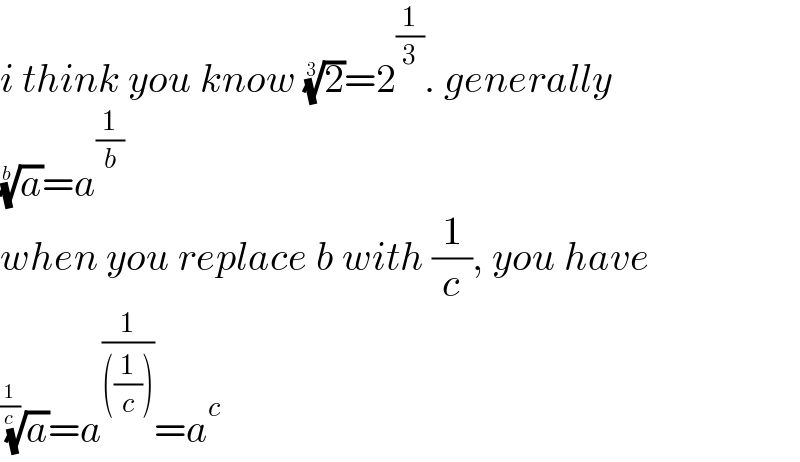
$${i}\:{think}\:{you}\:{know}\:\sqrt[{\mathrm{3}}]{\mathrm{2}}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} .\:{generally} \\ $$$$\sqrt[{{b}}]{{a}}={a}^{\frac{\mathrm{1}}{{b}}} \\ $$$${when}\:{you}\:{replace}\:{b}\:{with}\:\frac{\mathrm{1}}{{c}},\:{you}\:{have} \\ $$$$\sqrt[{\frac{\mathrm{1}}{{c}}}]{{a}}={a}^{\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{c}}\right)}} ={a}^{{c}} \\ $$
Commented by tabata last updated on 14/Oct/21

$${thank}\:{you}\:{sir}\: \\ $$
Commented by mr W last updated on 15/Oct/21

$${oui}! \\ $$
Commented by Sky_b last updated on 15/Oct/21
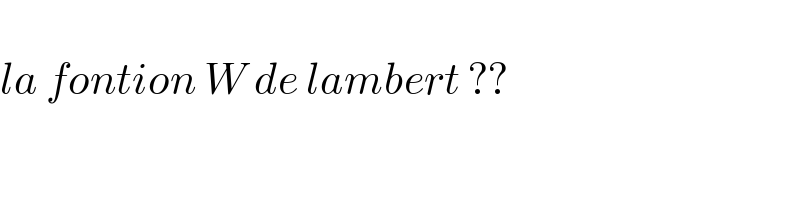
$$ \\ $$$${la}\:{fontion}\:{W}\:{de}\:{lambert}\:?? \\ $$$$ \\ $$$$ \\ $$
Commented by Ruuudiy last updated on 16/Oct/21
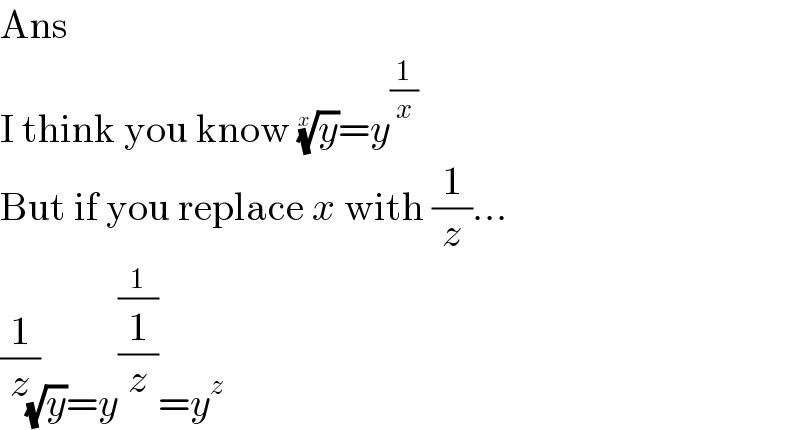
$$\mathrm{Ans} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{know}\:\sqrt[{{x}}]{{y}}={y}^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{But}\:\mathrm{if}\:\mathrm{you}\:\mathrm{replace}\:{x}\:\mathrm{with}\:\frac{\mathrm{1}}{{z}}… \\ $$$$\sqrt[{\frac{\mathrm{1}}{{z}}}]{{y}}={y}^{\frac{\mathrm{1}}{\frac{\mathrm{1}}{{z}}}} ={y}^{{z}} \\ $$
