Menu Close

solve-x-3-3x-2-1-0-

Tinku Tara 0 Comments
Pin




Question Number 122783 by mathocean1 last updated on 19/Nov/20
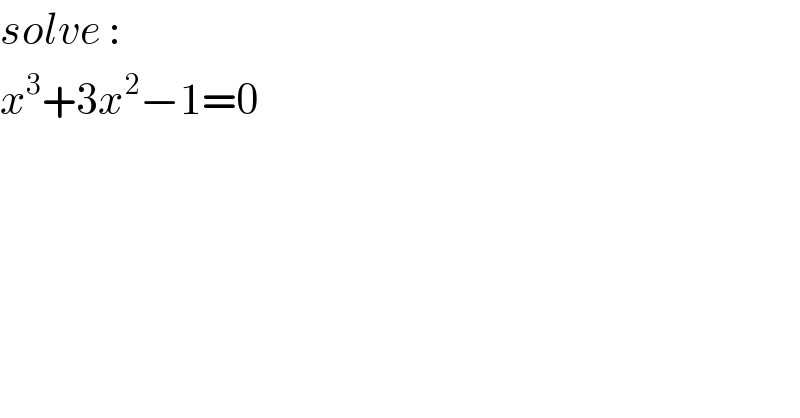
solve : x^3 +3x^2 −1=0
$${solve}\:: \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Nov/20
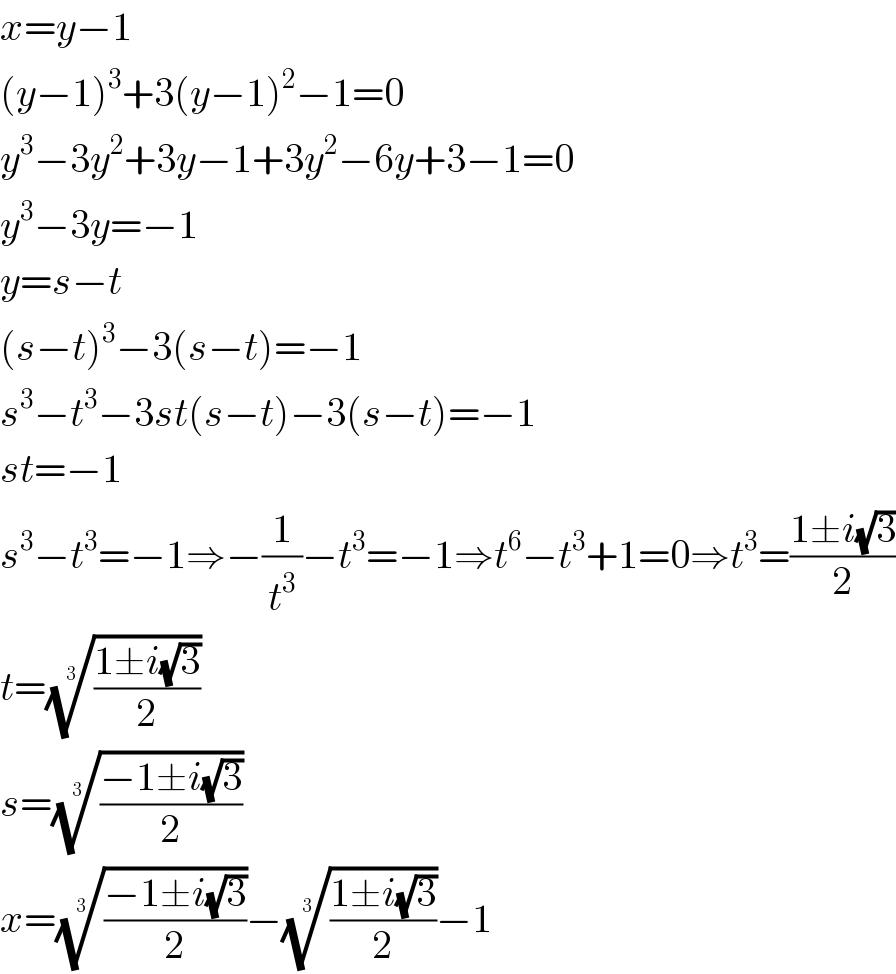
x=y−1 (y−1)^3 +3(y−1)^2 −1=0 y^3 −3y^2 +3y−1+3y^2 −6y+3−1=0 y^3 −3y=−1 y=s−t (s−t)^3 −3(s−t)=−1 s^3 −t^3 −3st(s−t)−3(s−t)=−1 st=−1 s^3 −t^3 =−1⇒−(1/t^3 )−t^3 =−1⇒t^6 −t^3 +1=0⇒t^3 =((1±i(√3))/2) t=(((1±i(√3))/2))^(1/3) s=(((−1±i(√3))/2))^(1/3) x=(((−1±i(√3))/2))^(1/3) −(((1±i(√3))/2))^(1/3) −1
$${x}={y}−\mathrm{1} \\ $$$$\left({y}−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{3}\left({y}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} −\mathrm{3}{y}^{\mathrm{2}} +\mathrm{3}{y}−\mathrm{1}+\mathrm{3}{y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{3}−\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} −\mathrm{3}{y}=−\mathrm{1}\:\:\:\:\:\:\: \\ $$$${y}={s}−{t}\:\:\:\:\:\: \\ $$$$\left({s}−{t}\right)^{\mathrm{3}} −\mathrm{3}\left({s}−{t}\right)=−\mathrm{1} \\ $$$${s}^{\mathrm{3}} −{t}^{\mathrm{3}} −\mathrm{3}{st}\left({s}−{t}\right)−\mathrm{3}\left({s}−{t}\right)=−\mathrm{1} \\ $$$${st}=−\mathrm{1} \\ $$$${s}^{\mathrm{3}} −{t}^{\mathrm{3}} =−\mathrm{1}\Rightarrow−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−{t}^{\mathrm{3}} =−\mathrm{1}\Rightarrow{t}^{\mathrm{6}} −{t}^{\mathrm{3}} +\mathrm{1}=\mathrm{0}\Rightarrow{t}^{\mathrm{3}} =\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${t}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$${s}=\sqrt[{\mathrm{3}}]{\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}−\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Nov/20
Generally ax^3 +bx^2 +cx+d=0 then depressed equation substitute x=y−(b/(3a)) a(y−(b/(3a)))^3 +b(y−(b/(3a)))^2 +c(y−(b/(3a)))+d=0 ay^3 −by(y−(b/(3a)))−(b^3 /(27a^2 ))+by^2 −((2b^2 y)/(3a))+(b^3 /(9a^2 ))+cy−((bc)/(3a))+d=0 ay^3 +((b^2 y)/(3a))+((2b^3 )/(27a^2 ))−((2b^2 y+bc)/(3a))+d=0 y^3 −y(b^2 /(3a^2 ))+(((2b^3 )/(27a^3 ))−((bc)/(3a^2 ))+(d/a))=0 y=s−t 3st=(b^2 /(3a^2 )) ⇒t=(b^2 /(9a^2 s)) s^3 −t^3 =−(((2b^3 )/(27a^3 ))−((bc)/(3a^2 ))+(d/a)) s^3 −(b^6 /(729a^6 s^3 ))=(((bc)/(3a^2 ))−((2b^3 )/(27a^3 ))−(d/a)) s^6 +(((2b^3 )/(27a^3 ))−((bc)/(3a^2 ))+(d/a))s^3 −(b^6 /(729a^6 ))=0 s=(((((bc)/(3a^2 ))−((2b^3 )/(27a^3 ))−(d/a)±(√((((bc)/(3a^2 ))−((2b^3 )/(27a^2 ))−(d/a))^2 +((4b^6 )/(729a^6 )))))/2))^(1/3) t=(((((2b^3 )/(27a^3 ))−((bc)/(3a^2 ))+(d/a)±(√((((bc)/(3a^2 ))−((2b^3 )/(27a^2 ))−(d/a))^2 +((4b^6 )/(729a^6 )))))/2))^(1/3) x=s−t+(b/(3a))
$${Generally} \\ $$$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$${then}\:{depressed}\:{equation} \\ $$$${substitute}\:{x}={y}−\frac{{b}}{\mathrm{3}{a}} \\ $$$${a}\left({y}−\frac{{b}}{\mathrm{3}{a}}\right)^{\mathrm{3}} +{b}\left({y}−\frac{{b}}{\mathrm{3}{a}}\right)^{\mathrm{2}} +{c}\left({y}−\frac{{b}}{\mathrm{3}{a}}\right)+{d}=\mathrm{0} \\ $$$${ay}^{\mathrm{3}} −{by}\left({y}−\frac{{b}}{\mathrm{3}{a}}\right)−\frac{{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{2}} }+{by}^{\mathrm{2}} −\frac{\mathrm{2}{b}^{\mathrm{2}} {y}}{\mathrm{3}{a}}+\frac{{b}^{\mathrm{3}} }{\mathrm{9}{a}^{\mathrm{2}} }+{cy}−\frac{{bc}}{\mathrm{3}{a}}+{d}=\mathrm{0} \\ $$$${ay}^{\mathrm{3}} +\frac{{b}^{\mathrm{2}} {y}}{\mathrm{3}{a}}+\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{2}} }−\frac{\mathrm{2}{b}^{\mathrm{2}} {y}+{bc}}{\mathrm{3}{a}}+{d}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} −{y}\frac{{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }+\left(\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }−\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{{d}}{{a}}\right)=\mathrm{0} \\ $$$${y}={s}−{t}\:\: \\ $$$$\mathrm{3}{st}=\frac{{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }\:\Rightarrow{t}=\frac{{b}^{\mathrm{2}} }{\mathrm{9}{a}^{\mathrm{2}} {s}} \\ $$$${s}^{\mathrm{3}} −{t}^{\mathrm{3}} =−\left(\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }−\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{{d}}{{a}}\right) \\ $$$${s}^{\mathrm{3}} −\frac{{b}^{\mathrm{6}} }{\mathrm{729}{a}^{\mathrm{6}} {s}^{\mathrm{3}} }=\left(\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }−\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }−\frac{{d}}{{a}}\right) \\ $$$${s}^{\mathrm{6}} +\left(\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }−\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{{d}}{{a}}\right){s}^{\mathrm{3}} −\frac{{b}^{\mathrm{6}} }{\mathrm{729}{a}^{\mathrm{6}} }=\mathrm{0} \\ $$$${s}=\sqrt[{\mathrm{3}}]{\frac{\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }−\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }−\frac{{d}}{{a}}\pm\sqrt{\left(\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }−\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{2}} }−\frac{{d}}{{a}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{b}^{\mathrm{6}} }{\mathrm{729}{a}^{\mathrm{6}} }}}{\mathrm{2}}} \\ $$$${t}=\sqrt[{\mathrm{3}}]{\frac{\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }−\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{{d}}{{a}}\pm\sqrt{\left(\frac{{bc}}{\mathrm{3}{a}^{\mathrm{2}} }−\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{2}} }−\frac{{d}}{{a}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{b}^{\mathrm{6}} }{\mathrm{729}{a}^{\mathrm{6}} }}}{\mathrm{2}}} \\ $$$${x}={s}−{t}+\frac{{b}}{\mathrm{3}{a}} \\ $$$$ \\ $$$$ \\ $$
Commented by MJS_new last updated on 19/Nov/20
Cardano′s Solution is not valid in these cases x^3 +px+q=0 D=(p^3 /(27))+(q^2 /4)<0 here we need the Trigonometric Solution as MrW showed
$$\mathrm{Cardano}'\mathrm{s}\:\mathrm{Solution}\:\mathrm{is}\:{not}\:\mathrm{valid}\:\mathrm{in}\:\mathrm{these}\:\mathrm{cases} \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{0} \\ $$$$\mathrm{here}\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{Trigonometric}\:\mathrm{Solution} \\ $$$$\mathrm{as}\:\mathrm{MrW}\:\mathrm{showed} \\ $$
Commented by Tawa11 last updated on 06/Nov/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 19/Nov/20
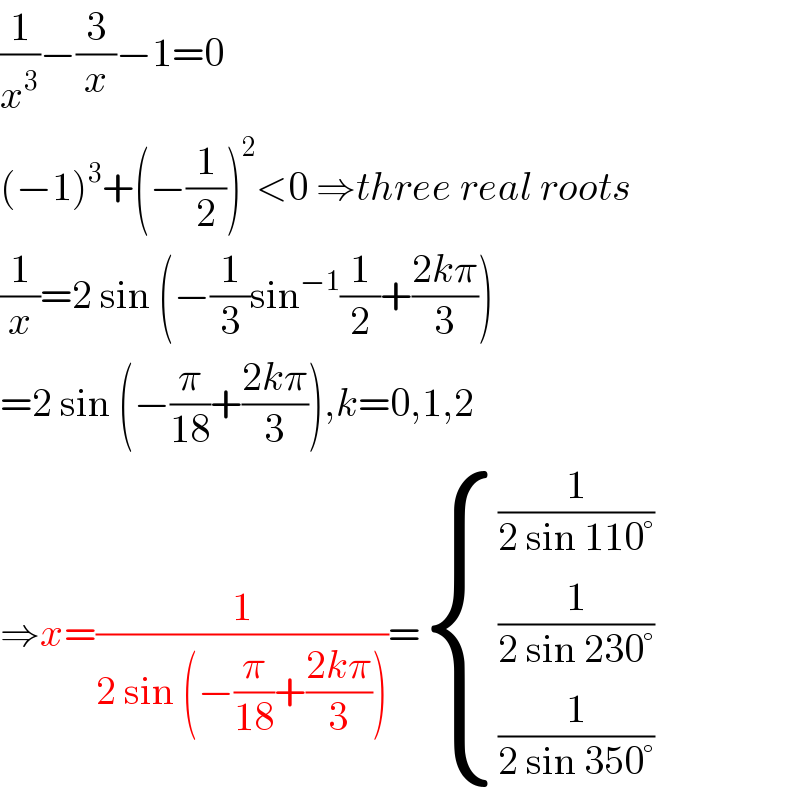
(1/x^3 )−(3/x)−1=0 (−1)^3 +(−(1/2))^2 <0 ⇒three real roots (1/x)=2 sin (−(1/3)sin^(−1) (1/2)+((2kπ)/3)) =2 sin (−(π/(18))+((2kπ)/3)),k=0,1,2 ⇒x=(1/(2 sin (−(π/(18))+((2kπ)/3))))= { ((1/(2 sin 110°))),((1/(2 sin 230°))),((1/(2 sin 350°))) :}
$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\frac{\mathrm{3}}{{x}}−\mathrm{1}=\mathrm{0} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{3}} +\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} <\mathrm{0}\:\Rightarrow{three}\:{real}\:{roots} \\ $$$$\frac{\mathrm{1}}{{x}}=\mathrm{2}\:\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}\:\left(−\frac{\pi}{\mathrm{18}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right),{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\left(−\frac{\pi}{\mathrm{18}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)}=\begin{cases}{\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{110}°}}\\{\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{230}°}}\\{\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{350}°}}\end{cases} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *