Question Number 169287 by cortano1 last updated on 28/Apr/22
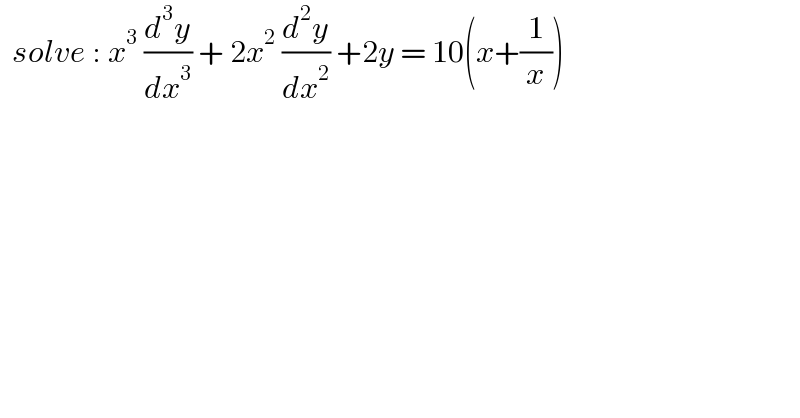
$$\:\:{solve}\::\:{x}^{\mathrm{3}} \:\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }\:+\:\mathrm{2}{x}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\mathrm{2}{y}\:=\:\mathrm{10}\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$
Commented by infinityaction last updated on 01/May/22

$$\:\:\:\:\:{let}\:{z}\:=\:\mathrm{log}\:_{\boldsymbol{{e}}} {x}\:\Rightarrow\:{x}\:=\:{e}^{\boldsymbol{{z}}} \\ $$$$\:\:\:\left\{{D}\left({D}−\mathrm{1}\right)\left({D}−\mathrm{2}\right)\:+\:\mathrm{2}{D}\left({D}−\mathrm{1}\right)\:+\:\mathrm{2}\right\}{y}\:=\:\mathrm{10}\left({e}^{\boldsymbol{{z}}\:} +{e}^{−{z}} \right) \\ $$$$\:\:\:\:\:\:\:\:{where}\:\frac{{d}}{{dz}}\:=\:{D} \\ $$$${A}\mathrm{uxiliary}\:\:\mathrm{Equation} \\ $$$$\:\:\:\:\:\:\:\:\:{m}^{\mathrm{3}} −{m}^{\mathrm{2}} +\mathrm{2}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −\mathrm{2}{m}+\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{m}\:=\:−\mathrm{1},\mathrm{1}\underset{−} {+}{i} \\ $$$$\:\:\:\:\:\:\boldsymbol{{C}}.\boldsymbol{{F}}\:=\:\boldsymbol{{c}}_{\mathrm{1}} \boldsymbol{{e}}^{−\boldsymbol{{x}}} +\boldsymbol{{e}}^{\boldsymbol{{z}}} \left(\boldsymbol{{c}}_{\mathrm{2}} \boldsymbol{\mathrm{cos}}\:\boldsymbol{{z}}+\:\boldsymbol{{c}}_{\mathrm{3}} \boldsymbol{\mathrm{sin}}\:\boldsymbol{{z}}\right) \\ $$$$\:\:\:\:\:\:\boldsymbol{{C}}.\boldsymbol{{F}}\:\:\:\:=\:\:\boldsymbol{{c}}_{\mathrm{1}} \boldsymbol{{x}}^{−\mathrm{1}} \:+\:\boldsymbol{{x}}\left\{\boldsymbol{{c}}_{\mathrm{2}} \boldsymbol{\mathrm{cos}}\:\left(\boldsymbol{\mathrm{log}}\:\boldsymbol{{x}}\right)\:+\:\boldsymbol{{c}}_{\mathrm{3}} \boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{\mathrm{log}}\:\boldsymbol{{x}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{P}}.\boldsymbol{{I}}\:=\:\frac{\mathrm{1}}{\left(\boldsymbol{{D}}+\mathrm{1}\right)\left(\boldsymbol{{D}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{D}}+\mathrm{2}\right)}\mathrm{10}\left(\boldsymbol{{e}}^{\boldsymbol{{z}}} \:+\:\boldsymbol{{e}}^{−\boldsymbol{{z}}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{P}}.\boldsymbol{{I}}\:=\:\mathrm{10}\left\{\frac{\mathrm{1}}{\left(\boldsymbol{{D}}+\mathrm{1}\right)\left(\boldsymbol{{D}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{D}}+\mathrm{2}\right)}\boldsymbol{{e}}^{\boldsymbol{{z}}} +\frac{\mathrm{1}}{\left(\boldsymbol{{D}}+\mathrm{1}\right)\left(\boldsymbol{{D}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{D}}+\mathrm{2}\right)}\boldsymbol{{e}}^{−\boldsymbol{{z}}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{P}.{I}\:\:\:\:\:\:=\:\:\:\:\mathrm{10}\left\{\frac{{e}^{\boldsymbol{{z}}} }{\mathrm{2}}\:+\:\frac{\mathrm{1}}{{D}+\mathrm{1}}\centerdot\frac{{e}^{−\boldsymbol{{z}}} }{\mathrm{1}+\mathrm{2}+\mathrm{2}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{P}.{I}\:\:\:\:=\mathrm{10}\left\{\frac{{e}^{{z}} }{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{5}}\:\frac{\mathrm{1}}{\left({D}+\mathrm{1}\right)}{e}^{−{z}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:{P}.{I}\:\:=\mathrm{10}\left\{\frac{{e}^{−\boldsymbol{{z}}} }{\mathrm{2}}\:+\:\frac{{e}^{−\boldsymbol{{z}}} }{\mathrm{5}}\:\frac{\mathrm{1}}{\left({D}−\mathrm{1}+\mathrm{1}\right)}\centerdot\mathrm{1}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:{P}.{I}\:\:\:\:=\:\:\mathrm{10}\left\{\frac{{e}^{\boldsymbol{{z}}} }{\mathrm{2}}\:+\frac{{ze}^{−\boldsymbol{{z}}} }{\mathrm{5}}\right\}\:=\:\mathrm{5}{x}+\mathrm{2}{x}^{−\mathrm{1}} \mathrm{log}\:{x} \\ $$$$\:\:\:\boldsymbol{{y}}\:=\:\boldsymbol{{c}}_{\mathrm{1}} \boldsymbol{{x}}^{−\mathrm{1}} +\boldsymbol{{x}}\left\{\boldsymbol{{c}}_{\mathrm{2}} \boldsymbol{\mathrm{cos}}\:\left(\boldsymbol{\mathrm{log}}\:\boldsymbol{{x}}\right)+\boldsymbol{{c}}_{\mathrm{3}} \boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{\mathrm{log}}\:\boldsymbol{{x}}\right)\right\}+\mathrm{5}\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{x}}^{−\mathrm{1}} \boldsymbol{\mathrm{log}}\:\boldsymbol{{x}} \\ $$$$ \\ $$$$\:\: \\ $$
Commented by cortano1 last updated on 28/Apr/22

$${nice} \\ $$
