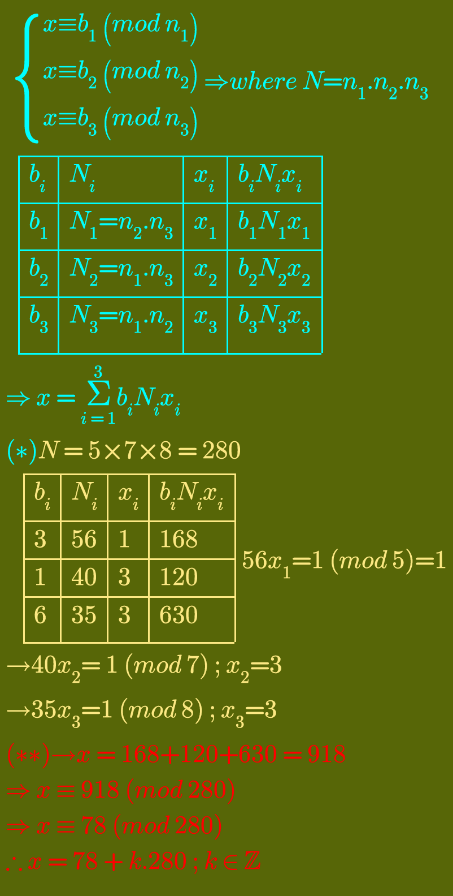Question Number 109410 by bobhans last updated on 23/Aug/20
$${solve}\:\begin{cases}{{x}\equiv\mathrm{3}\:\left({mod}\:\mathrm{5}\right)}\\{{x}\equiv\:\mathrm{1}\:\left({mod}\:\mathrm{7}\right)}\\{{x}\:\equiv\:\mathrm{6}\:\left({mod}\:\mathrm{8}\right)}\end{cases} \\ $$
Commented by bobhans last updated on 24/Aug/20
$${thank}\:{you}\:{all}\:{master} \\ $$
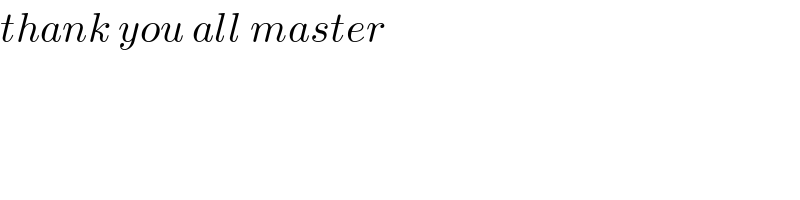
Answered by 1xx last updated on 23/Aug/20
![solve { ((x≡3 (mod 5))),((x≡ 1 (mod 7))),((x ≡ 6 (mod 8))) :} x=5m+3=7n+1=8p+6 5m=7n−2=7n^′ +5=7n^(′′) +14+5=7n^(′′) +19 5m=8p+3=8p^′ +16+3=8p^′ +19 7n^(′′) =8p^′ =7×8=56 5m=56+19=75 x_1 =75+3=78=7×11+1=8×9+6 x_1 =78 5m=56k+19=56k+15+4=(56k+4)+3×5 (56k+4)≡0(mod 5) (55k+k+4)≡0(mod 5) (k+4)≡0(mod 5) k=5t−4 x=56k+4+3×5+3=56k+22 x=56(5t−4)+22 x=280t−202 t∈Z another way: ... ... x_1 =78 ∵ (5,7,8)=0 ∴ [5,7,8]=5×7×8=280 x=x_1 +n[5,7,8]=78+280n n∈Z](https://www.tinkutara.com/question/Q109417.png)
$${solve}\:\begin{cases}{{x}\equiv\mathrm{3}\:\left({mod}\:\mathrm{5}\right)}\\{{x}\equiv\:\mathrm{1}\:\left({mod}\:\mathrm{7}\right)}\\{{x}\:\equiv\:\mathrm{6}\:\left({mod}\:\mathrm{8}\right)}\end{cases} \\ $$$${x}=\mathrm{5}{m}+\mathrm{3}=\mathrm{7}{n}+\mathrm{1}=\mathrm{8}{p}+\mathrm{6} \\ $$$$\mathrm{5}{m}=\mathrm{7}{n}−\mathrm{2}=\mathrm{7}{n}^{'} +\mathrm{5}=\mathrm{7}{n}^{''} +\mathrm{14}+\mathrm{5}=\mathrm{7}{n}^{''} +\mathrm{19} \\ $$$$\mathrm{5}{m}=\mathrm{8}{p}+\mathrm{3}=\mathrm{8}{p}^{'} +\mathrm{16}+\mathrm{3}=\mathrm{8}{p}^{'} +\mathrm{19} \\ $$$$\mathrm{7}{n}^{''} =\mathrm{8}{p}^{'} =\mathrm{7}×\mathrm{8}=\mathrm{56} \\ $$$$\mathrm{5}{m}=\mathrm{56}+\mathrm{19}=\mathrm{75} \\ $$$${x}_{\mathrm{1}} =\mathrm{75}+\mathrm{3}=\mathrm{78}=\mathrm{7}×\mathrm{11}+\mathrm{1}=\mathrm{8}×\mathrm{9}+\mathrm{6} \\ $$$${x}_{\mathrm{1}} =\mathrm{78} \\ $$$$\mathrm{5}{m}=\mathrm{56}{k}+\mathrm{19}=\mathrm{56}{k}+\mathrm{15}+\mathrm{4}=\left(\mathrm{56}{k}+\mathrm{4}\right)+\mathrm{3}×\mathrm{5} \\ $$$$\left(\mathrm{56}{k}+\mathrm{4}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$$\left(\mathrm{55}{k}+{k}+\mathrm{4}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$$\left({k}+\mathrm{4}\right)\equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$${k}=\mathrm{5}{t}−\mathrm{4} \\ $$$${x}=\mathrm{56}{k}+\mathrm{4}+\mathrm{3}×\mathrm{5}+\mathrm{3}=\mathrm{56}{k}+\mathrm{22} \\ $$$${x}=\mathrm{56}\left(\mathrm{5}{t}−\mathrm{4}\right)+\mathrm{22} \\ $$$${x}=\mathrm{280}{t}−\mathrm{202}\:\:\:{t}\in{Z} \\ $$$${another}\:{way}: \\ $$$$…\:… \\ $$$${x}_{\mathrm{1}} =\mathrm{78} \\ $$$$\because\:\left(\mathrm{5},\mathrm{7},\mathrm{8}\right)=\mathrm{0} \\ $$$$\therefore\:\left[\mathrm{5},\mathrm{7},\mathrm{8}\right]=\mathrm{5}×\mathrm{7}×\mathrm{8}=\mathrm{280} \\ $$$${x}={x}_{\mathrm{1}} +{n}\left[\mathrm{5},\mathrm{7},\mathrm{8}\right]=\mathrm{78}+\mathrm{280}{n}\:\:\:\:{n}\in{Z} \\ $$
Answered by floor(10²Eta[1]) last updated on 23/Aug/20
$$\mathrm{x}\equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{8}\right)\Rightarrow\mathrm{x}=\mathrm{8a}+\mathrm{6} \\ $$$$\mathrm{8a}+\mathrm{6}\equiv\mathrm{3}\left(\mathrm{mod}\:\mathrm{5}\right)\Rightarrow\mathrm{a}\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{5}\right)\therefore\mathrm{a}=\mathrm{5b}+\mathrm{4} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{8}\left(\mathrm{5b}+\mathrm{4}\right)+\mathrm{6}=\mathrm{40b}+\mathrm{38} \\ $$$$\mathrm{40b}+\mathrm{38}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{7}\right)\Rightarrow\mathrm{b}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{7}\right)\therefore\mathrm{b}=\mathrm{7c}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{40}\left(\mathrm{7c}+\mathrm{1}\right)+\mathrm{38} \\ $$$$\therefore\:\mathrm{x}=\mathrm{280c}+\mathrm{78},\:\mathrm{c}\in\mathbb{Z} \\ $$$$\mathrm{x}\in\left\{…,−\mathrm{482},\:−\mathrm{202},\:\mathrm{78},\:\mathrm{358},…\right\} \\ $$
Commented by 1xx last updated on 23/Aug/20
$${Yes}.{I}\:{forgot}\:{x}<\mathrm{0}.\:{Thank}\:{you}! \\ $$
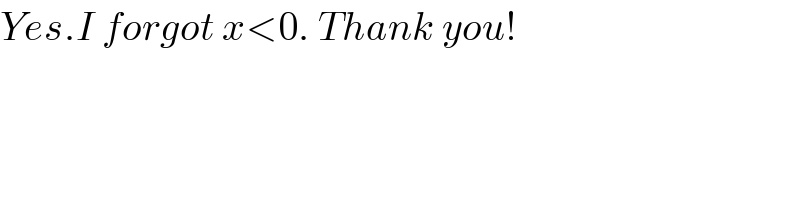
Answered by john santu last updated on 24/Aug/20
