Menu Close

Solve-x-4-log-5-50x-x-6-

Tinku Tara 0 Comments
Pin




Question Number 52007 by Tawa1 last updated on 02/Jan/19
Solve: ((x/4))^(log_5 50x) = x^6
$$\mathrm{Solve}:\:\:\:\:\:\:\:\:\:\:\left(\frac{\boldsymbol{\mathrm{x}}}{\mathrm{4}}\right)^{\boldsymbol{\mathrm{log}}_{\mathrm{5}} \mathrm{50}\boldsymbol{\mathrm{x}}} \:\:\:=\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{6}} \\ $$
Answered by MJS last updated on 02/Jan/19
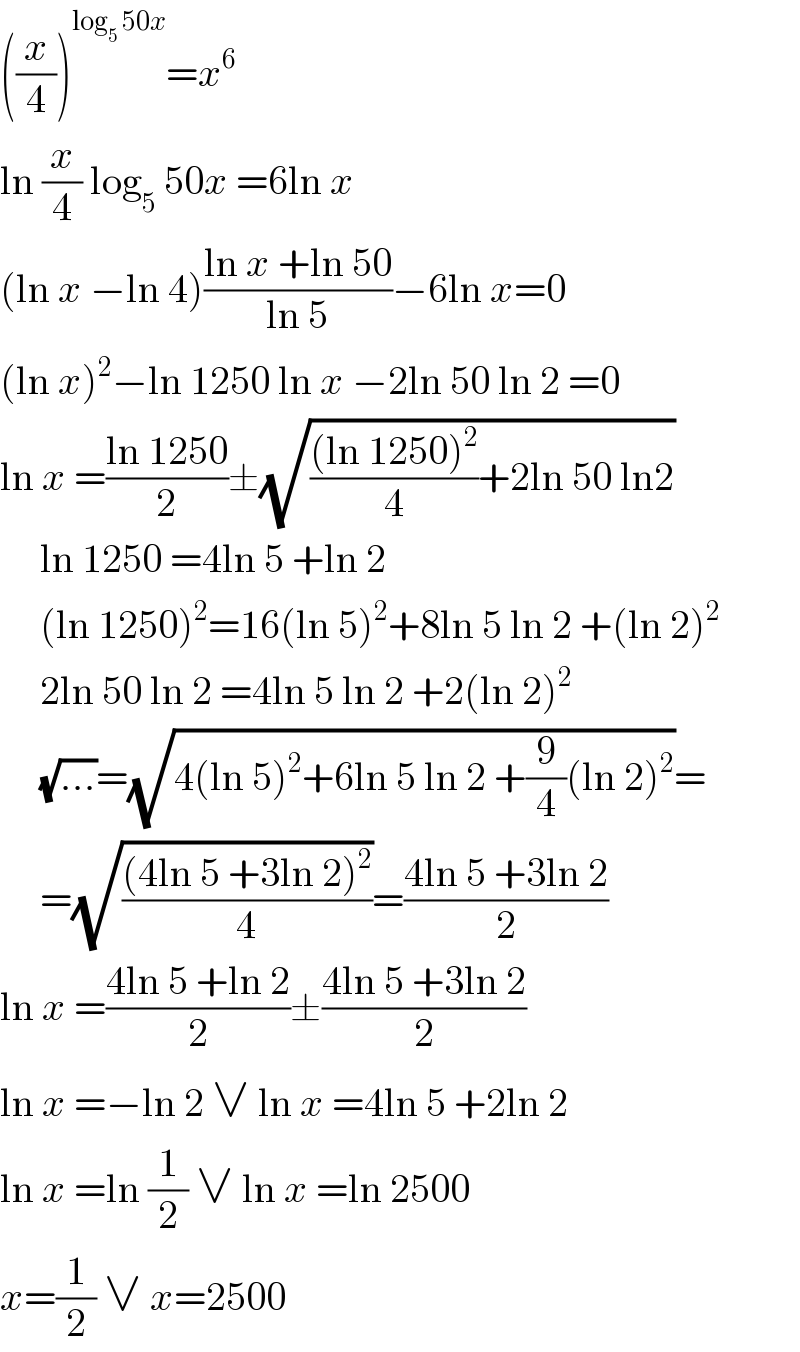
((x/4))^(log_5 50x) =x^6 ln (x/4) log_5 50x =6ln x (ln x −ln 4)((ln x +ln 50)/(ln 5))−6ln x=0 (ln x)^2 −ln 1250 ln x −2ln 50 ln 2 =0 ln x =((ln 1250)/2)±(√((((ln 1250)^2 )/4)+2ln 50 ln2)) ln 1250 =4ln 5 +ln 2 (ln 1250)^2 =16(ln 5)^2 +8ln 5 ln 2 +(ln 2)^2 2ln 50 ln 2 =4ln 5 ln 2 +2(ln 2)^2 (√(...))=(√(4(ln 5)^2 +6ln 5 ln 2 +(9/4)(ln 2)^2 ))= =(√(((4ln 5 +3ln 2)^2 )/4))=((4ln 5 +3ln 2)/2) ln x =((4ln 5 +ln 2)/2)±((4ln 5 +3ln 2)/2) ln x =−ln 2 ∨ ln x =4ln 5 +2ln 2 ln x =ln (1/2) ∨ ln x =ln 2500 x=(1/2) ∨ x=2500
$$\left(\frac{{x}}{\mathrm{4}}\right)^{\mathrm{log}_{\mathrm{5}} \:\mathrm{50}{x}} ={x}^{\mathrm{6}} \\ $$$$\mathrm{ln}\:\frac{{x}}{\mathrm{4}}\:\mathrm{log}_{\mathrm{5}} \:\mathrm{50}{x}\:=\mathrm{6ln}\:{x} \\ $$$$\left(\mathrm{ln}\:{x}\:−\mathrm{ln}\:\mathrm{4}\right)\frac{\mathrm{ln}\:{x}\:+\mathrm{ln}\:\mathrm{50}}{\mathrm{ln}\:\mathrm{5}}−\mathrm{6ln}\:{x}=\mathrm{0} \\ $$$$\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} −\mathrm{ln}\:\mathrm{1250}\:\mathrm{ln}\:{x}\:−\mathrm{2ln}\:\mathrm{50}\:\mathrm{ln}\:\mathrm{2}\:=\mathrm{0} \\ $$$$\mathrm{ln}\:{x}\:=\frac{\mathrm{ln}\:\mathrm{1250}}{\mathrm{2}}\pm\sqrt{\frac{\left(\mathrm{ln}\:\mathrm{1250}\right)^{\mathrm{2}} }{\mathrm{4}}+\mathrm{2ln}\:\mathrm{50}\:\mathrm{ln2}} \\ $$$$\:\:\:\:\:\mathrm{ln}\:\mathrm{1250}\:=\mathrm{4ln}\:\mathrm{5}\:+\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:\:\:\:\left(\mathrm{ln}\:\mathrm{1250}\right)^{\mathrm{2}} =\mathrm{16}\left(\mathrm{ln}\:\mathrm{5}\right)^{\mathrm{2}} +\mathrm{8ln}\:\mathrm{5}\:\mathrm{ln}\:\mathrm{2}\:+\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{2ln}\:\mathrm{50}\:\mathrm{ln}\:\mathrm{2}\:=\mathrm{4ln}\:\mathrm{5}\:\mathrm{ln}\:\mathrm{2}\:+\mathrm{2}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\sqrt{…}=\sqrt{\mathrm{4}\left(\mathrm{ln}\:\mathrm{5}\right)^{\mathrm{2}} +\mathrm{6ln}\:\mathrm{5}\:\mathrm{ln}\:\mathrm{2}\:+\frac{\mathrm{9}}{\mathrm{4}}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:=\sqrt{\frac{\left(\mathrm{4ln}\:\mathrm{5}\:+\mathrm{3ln}\:\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}}}=\frac{\mathrm{4ln}\:\mathrm{5}\:+\mathrm{3ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$$\mathrm{ln}\:{x}\:=\frac{\mathrm{4ln}\:\mathrm{5}\:+\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\pm\frac{\mathrm{4ln}\:\mathrm{5}\:+\mathrm{3ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$$\mathrm{ln}\:{x}\:=−\mathrm{ln}\:\mathrm{2}\:\vee\:\mathrm{ln}\:{x}\:=\mathrm{4ln}\:\mathrm{5}\:+\mathrm{2ln}\:\mathrm{2} \\ $$$$\mathrm{ln}\:{x}\:=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{2}}\:\vee\:\mathrm{ln}\:{x}\:=\mathrm{ln}\:\mathrm{2500} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\:\vee\:{x}=\mathrm{2500} \\ $$
Commented by Tawa1 last updated on 02/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jan/19
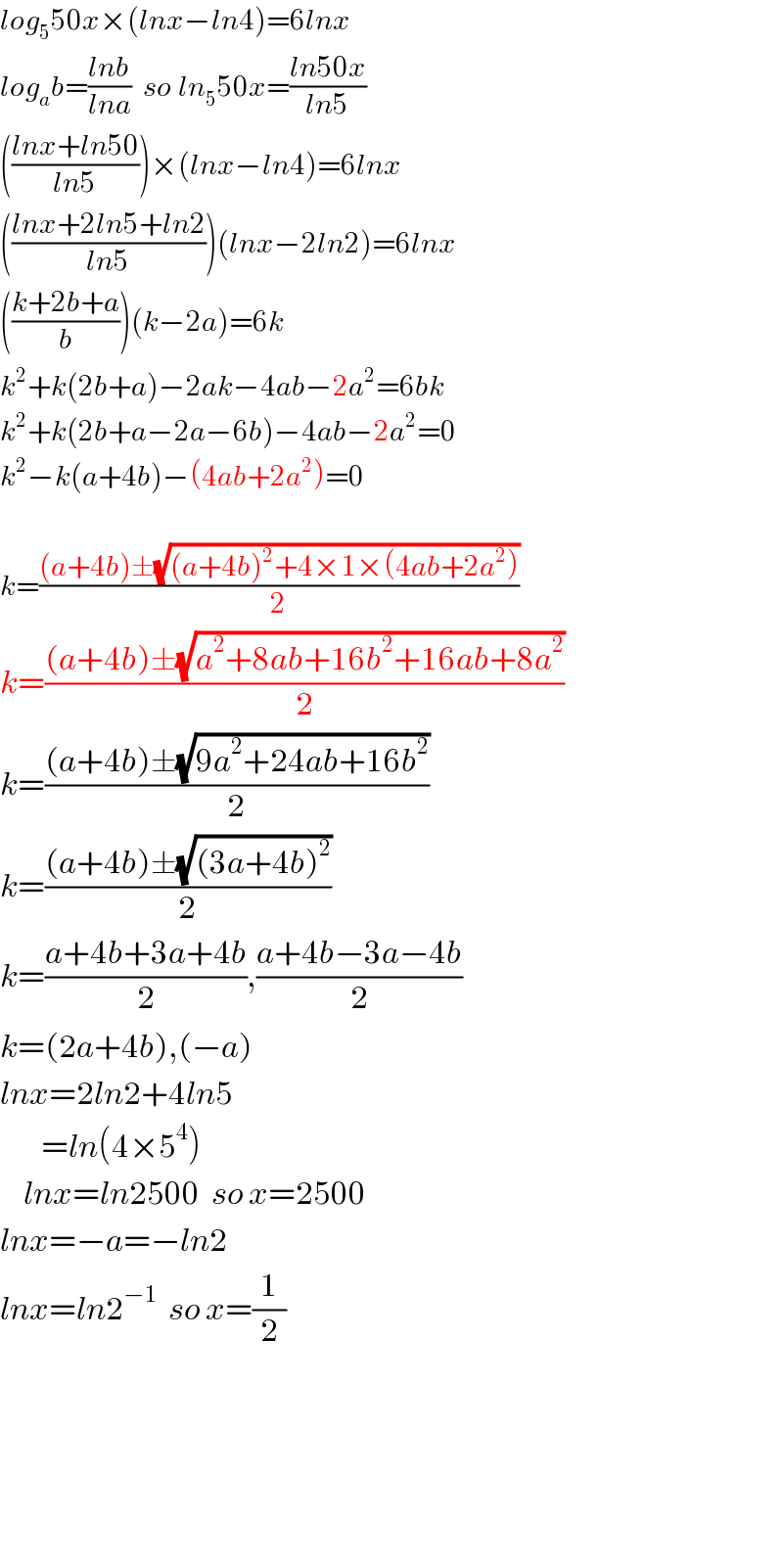
log_5 50x×(lnx−ln4)=6lnx log_a b=((lnb)/(lna)) so ln_5 50x=((ln50x)/(ln5)) (((lnx+ln50)/(ln5)))×(lnx−ln4)=6lnx (((lnx+2ln5+ln2)/(ln5)))(lnx−2ln2)=6lnx (((k+2b+a)/b))(k−2a)=6k k^2 +k(2b+a)−2ak−4ab−2a^2 =6bk k^2 +k(2b+a−2a−6b)−4ab−2a^2 =0 k^2 −k(a+4b)−(4ab+2a^2 )=0 k=(((a+4b)±(√((a+4b)^2 +4×1×(4ab+2a^2 ))))/2) k=(((a+4b)±(√(a^2 +8ab+16b^2 +16ab+8a^2 )))/2) k=(((a+4b)±(√(9a^2 +24ab+16b^2 )))/2) k=(((a+4b)±(√((3a+4b)^2 )))/2) k=((a+4b+3a+4b)/2),((a+4b−3a−4b)/2) k=(2a+4b),(−a) lnx=2ln2+4ln5 =ln(4×5^4 ) lnx=ln2500 so x=2500 lnx=−a=−ln2 lnx=ln2^(−1) so x=(1/2)
$${log}_{\mathrm{5}} \mathrm{50}{x}×\left({lnx}−{ln}\mathrm{4}\right)=\mathrm{6}{lnx} \\ $$$${log}_{{a}} {b}=\frac{{lnb}}{{lna}}\:\:{so}\:{ln}_{\mathrm{5}} \mathrm{50}{x}=\frac{{ln}\mathrm{50}{x}}{{ln}\mathrm{5}} \\ $$$$\left(\frac{{lnx}+{ln}\mathrm{50}}{{ln}\mathrm{5}}\right)×\left({lnx}−{ln}\mathrm{4}\right)=\mathrm{6}{lnx} \\ $$$$\left(\frac{{lnx}+\mathrm{2}{ln}\mathrm{5}+{ln}\mathrm{2}}{{ln}\mathrm{5}}\right)\left({lnx}−\mathrm{2}{ln}\mathrm{2}\right)=\mathrm{6}{lnx} \\ $$$$\left(\frac{{k}+\mathrm{2}{b}+{a}}{{b}}\right)\left({k}−\mathrm{2}{a}\right)=\mathrm{6}{k} \\ $$$${k}^{\mathrm{2}} +{k}\left(\mathrm{2}{b}+{a}\right)−\mathrm{2}{ak}−\mathrm{4}{ab}−\mathrm{2}{a}^{\mathrm{2}} =\mathrm{6}{bk} \\ $$$${k}^{\mathrm{2}} +{k}\left(\mathrm{2}{b}+{a}−\mathrm{2}{a}−\mathrm{6}{b}\right)−\mathrm{4}{ab}−\mathrm{2}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${k}^{\mathrm{2}} −{k}\left({a}+\mathrm{4}{b}\right)−\left(\mathrm{4}{ab}+\mathrm{2}{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$ \\ $$$${k}=\frac{\left({a}+\mathrm{4}{b}\right)\pm\sqrt{\left({a}+\mathrm{4}{b}\right)^{\mathrm{2}} +\mathrm{4}×\mathrm{1}×\left(\mathrm{4}{ab}+\mathrm{2}{a}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$${k}=\frac{\left({a}+\mathrm{4}{b}\right)\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{8}{ab}+\mathrm{16}{b}^{\mathrm{2}} +\mathrm{16}{ab}+\mathrm{8}{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${k}=\frac{\left({a}+\mathrm{4}{b}\right)\pm\sqrt{\mathrm{9}{a}^{\mathrm{2}} +\mathrm{24}{ab}+\mathrm{16}{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${k}=\frac{\left({a}+\mathrm{4}{b}\right)\pm\sqrt{\left(\mathrm{3}{a}+\mathrm{4}{b}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${k}=\frac{{a}+\mathrm{4}{b}+\mathrm{3}{a}+\mathrm{4}{b}}{\mathrm{2}},\frac{{a}+\mathrm{4}{b}−\mathrm{3}{a}−\mathrm{4}{b}}{\mathrm{2}} \\ $$$${k}=\left(\mathrm{2}{a}+\mathrm{4}{b}\right),\left(−{a}\right) \\ $$$${lnx}=\mathrm{2}{ln}\mathrm{2}+\mathrm{4}{ln}\mathrm{5} \\ $$$$\:\:\:\:\:\:\:={ln}\left(\mathrm{4}×\mathrm{5}^{\mathrm{4}} \right) \\ $$$$\:\:\:\:{lnx}={ln}\mathrm{2500}\:\:{so}\:{x}=\mathrm{2500} \\ $$$${lnx}=−{a}=−{ln}\mathrm{2} \\ $$$${lnx}={ln}\mathrm{2}^{−\mathrm{1}} \:\:{so}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 02/Jan/19
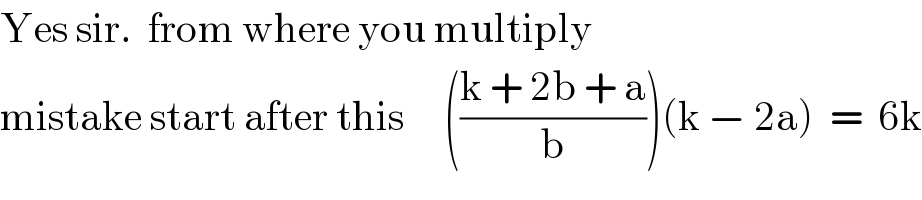
Yes sir. from where you multiply mistake start after this (((k + 2b + a)/b))(k − 2a) = 6k
$$\mathrm{Yes}\:\mathrm{sir}.\:\:\mathrm{from}\:\mathrm{where}\:\mathrm{you}\:\mathrm{multiply} \\ $$$$\mathrm{mistake}\:\mathrm{start}\:\mathrm{after}\:\mathrm{this}\:\:\:\:\:\left(\frac{\mathrm{k}\:+\:\mathrm{2b}\:+\:\mathrm{a}}{\mathrm{b}}\right)\left(\mathrm{k}\:−\:\mathrm{2a}\right)\:\:=\:\:\mathrm{6k} \\ $$
Commented by Tawa1 last updated on 02/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 02/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *