Question Number 171844 by Mikenice last updated on 21/Jun/22
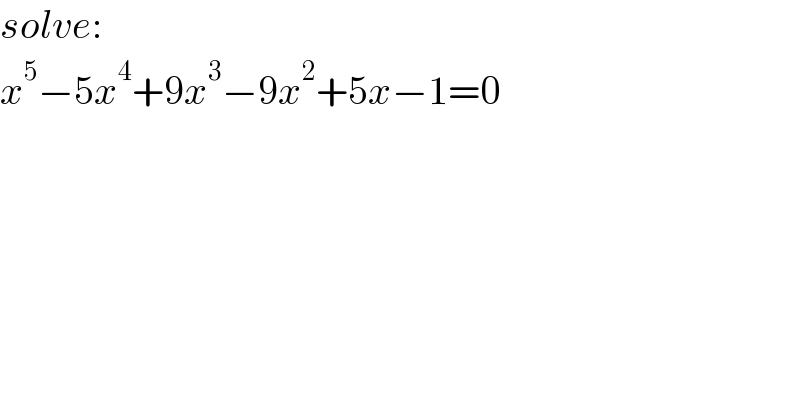
$${solve}: \\ $$$${x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} +\mathrm{9}{x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{1}=\mathrm{0} \\ $$
Answered by floor(10²Eta[1]) last updated on 21/Jun/22
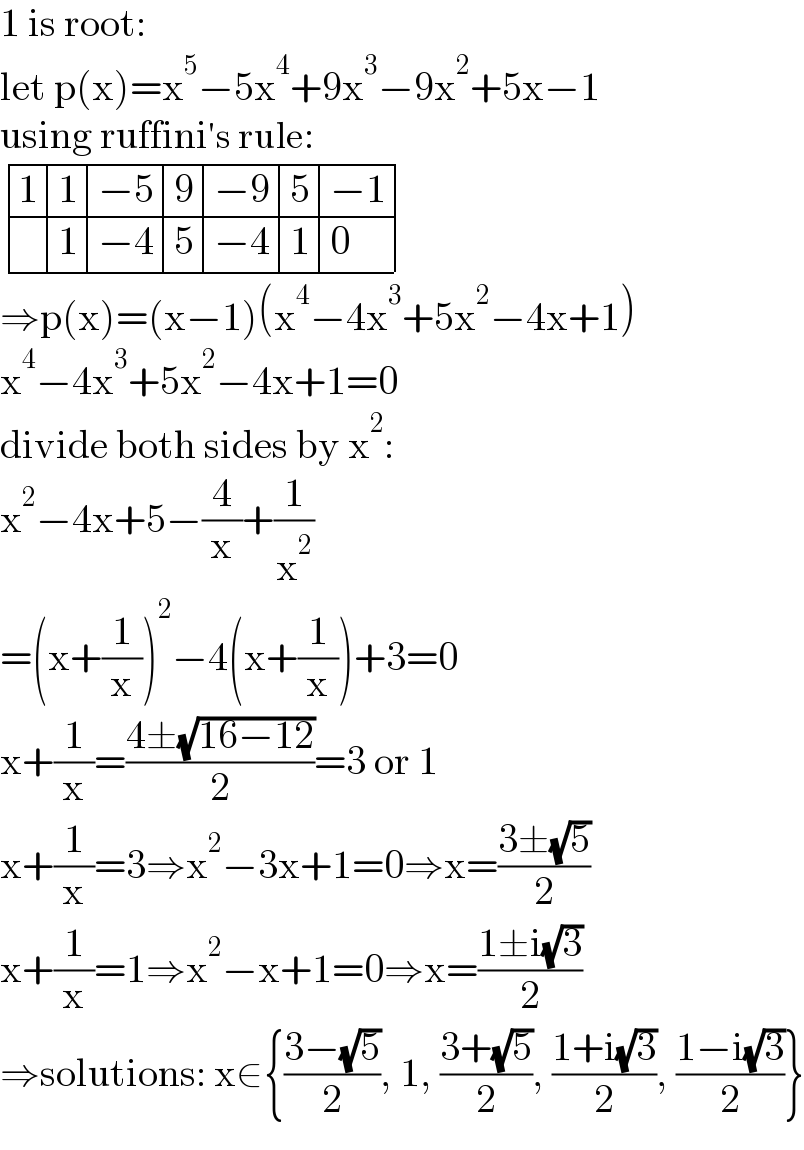
$$\mathrm{1}\:\mathrm{is}\:\mathrm{root}: \\ $$$$\mathrm{let}\:\mathrm{p}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{5}} −\mathrm{5x}^{\mathrm{4}} +\mathrm{9x}^{\mathrm{3}} −\mathrm{9x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{1} \\ $$$$\mathrm{using}\:\mathrm{ruffini}'\mathrm{s}\:\mathrm{rule}: \\ $$$$\begin{array}{|c|c|}{\mathrm{1}}&\hline{\mathrm{1}}&\hline{−\mathrm{5}}&\hline{\mathrm{9}}&\hline{−\mathrm{9}}&\hline{\mathrm{5}}&\hline{−\mathrm{1}}\\{}&\hline{\mathrm{1}}&\hline{−\mathrm{4}}&\hline{\mathrm{5}}&\hline{−\mathrm{4}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}\\\hline\end{array} \\ $$$$\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{3}} +\mathrm{5x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{3}} +\mathrm{5x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{divide}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:\mathrm{x}^{\mathrm{2}} : \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{5}−\frac{\mathrm{4}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{12}}}{\mathrm{2}}=\mathrm{3}\:\mathrm{or}\:\mathrm{1} \\ $$$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{3}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{solutions}:\:\mathrm{x}\in\left\{\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}},\:\mathrm{1},\:\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}},\:\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}},\:\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right\} \\ $$
Commented by Mikenice last updated on 21/Jun/22

$${thanks}\:{sir} \\ $$
