Question Number 104342 by bemath last updated on 21/Jul/20
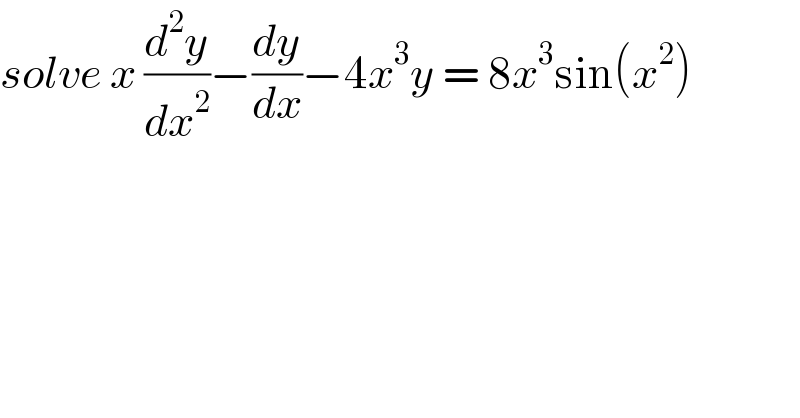
$${solve}\:{x}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\frac{{dy}}{{dx}}−\mathrm{4}{x}^{\mathrm{3}} {y}\:=\:\mathrm{8}{x}^{\mathrm{3}} \mathrm{sin}\left({x}^{\mathrm{2}} \right) \\ $$
Answered by bramlex last updated on 21/Jul/20
![multiplying both sides by x ⇒x^2 .(d^2 y/dx^2 )−x(dy/dx)−4x^4 y=8x^4 sin (x^2 )...(1) set x^2 = z → (dz/dx) = 2x (dy/dx) = (dy/dz).(dz/dx) = 2x (dy/dz)→ (dy/dx) = 2x.(dy/dz)...(2) (d^2 y/dx^2 ) = (d/dx)(2x (dy/dz)) = 2(dy/dz)+2x (d/dx)((dy/dx)) = 2(dy/dz) +2x (d/dz)((dy/dz)).(dz/dx)...(3) using (2) &(3) in (1) (→)x^2 [2(dy/dx)+4x^2 (d^2 y/dz^2 ) ]−x(2x(dy/dz)) −4x^4 y = 8x^4 sin (x^2 ) (→) 4x^4 ((d^2 y/dz^2 ) −y) = 8x^4 sin (z) (→) (d^2 y/dz^2 ) −y = 2sin (z) (→) (D^2 −1)y = 2sin (z) Homogenous part y_c = C_1 e^(−x) +C_2 e^x particular integral y_p = (1/(D^2 −1))(2sin (z))= −sin (z)=−sin (x^2 ) General solution ∴ y = C_1 e^(−x) +C_2 e^x −sin (x^2 ) ★](https://www.tinkutara.com/question/Q104345.png)
$${multiplying}\:{both}\:{sides}\:{by}\:{x} \\ $$$$\Rightarrow{x}^{\mathrm{2}} .\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−{x}\frac{{dy}}{{dx}}−\mathrm{4}{x}^{\mathrm{4}} {y}=\mathrm{8}{x}^{\mathrm{4}} \mathrm{sin}\:\left({x}^{\mathrm{2}} \right)…\left(\mathrm{1}\right) \\ $$$${set}\:{x}^{\mathrm{2}} \:=\:{z}\:\rightarrow\:\frac{{dz}}{{dx}}\:=\:\mathrm{2}{x}\: \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{dy}}{{dz}}.\frac{{dz}}{{dx}}\:=\:\mathrm{2}{x}\:\frac{{dy}}{{dz}}\rightarrow\:\frac{{dy}}{{dx}}\:=\:\mathrm{2}{x}.\frac{{dy}}{{dz}}…\left(\mathrm{2}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\frac{{d}}{{dx}}\left(\mathrm{2}{x}\:\frac{{dy}}{{dz}}\right)\:=\:\mathrm{2}\frac{{dy}}{{dz}}+\mathrm{2}{x}\:\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\frac{{dy}}{{dz}}\:+\mathrm{2}{x}\:\frac{{d}}{{dz}}\left(\frac{{dy}}{{dz}}\right).\frac{{dz}}{{dx}}…\left(\mathrm{3}\right) \\ $$$${using}\:\left(\mathrm{2}\right)\:\&\left(\mathrm{3}\right)\:{in}\:\left(\mathrm{1}\right) \\ $$$$\left(\rightarrow\right){x}^{\mathrm{2}} \left[\mathrm{2}\frac{{dy}}{{dx}}+\mathrm{4}{x}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {y}}{{dz}^{\mathrm{2}} }\:\right]−{x}\left(\mathrm{2}{x}\frac{{dy}}{{dz}}\right) \\ $$$$−\mathrm{4}{x}^{\mathrm{4}} {y}\:=\:\mathrm{8}{x}^{\mathrm{4}} \:\mathrm{sin}\:\left({x}^{\mathrm{2}} \right) \\ $$$$\left(\rightarrow\right)\:\mathrm{4}{x}^{\mathrm{4}} \:\left(\frac{{d}^{\mathrm{2}} {y}}{{dz}^{\mathrm{2}} }\:−{y}\right)\:=\:\mathrm{8}{x}^{\mathrm{4}} \:\mathrm{sin}\:\left({z}\right) \\ $$$$\left(\rightarrow\right)\:\frac{{d}^{\mathrm{2}} {y}}{{dz}^{\mathrm{2}} }\:−{y}\:=\:\mathrm{2sin}\:\left({z}\right)\: \\ $$$$\left(\rightarrow\right)\:\left({D}^{\mathrm{2}} −\mathrm{1}\right){y}\:=\:\mathrm{2sin}\:\left({z}\right) \\ $$$${Homogenous}\:{part} \\ $$$${y}_{{c}} \:=\:{C}_{\mathrm{1}} {e}^{−{x}} +{C}_{\mathrm{2}} {e}^{{x}} \\ $$$${particular}\:{integral} \\ $$$${y}_{{p}} =\:\frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{2sin}\:\left({z}\right)\right)=\:−\mathrm{sin}\:\left({z}\right)=−\mathrm{sin}\:\left({x}^{\mathrm{2}} \right) \\ $$$$\mathcal{G}{eneral}\:{solution} \\ $$$$\therefore\:{y}\:=\:{C}_{\mathrm{1}} {e}^{−{x}} +{C}_{\mathrm{2}} {e}^{{x}} −\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)\:\bigstar \\ $$
Commented by bemath last updated on 21/Jul/20

$${great}…{nice}\: \\ $$
