Question Number 172259 by mr W last updated on 25/Jun/22

$${solve} \\ $$$${x}^{{x}} =\mathrm{3}^{\frac{\mathrm{1}}{{x}}} \\ $$
Answered by mr W last updated on 25/Jun/22
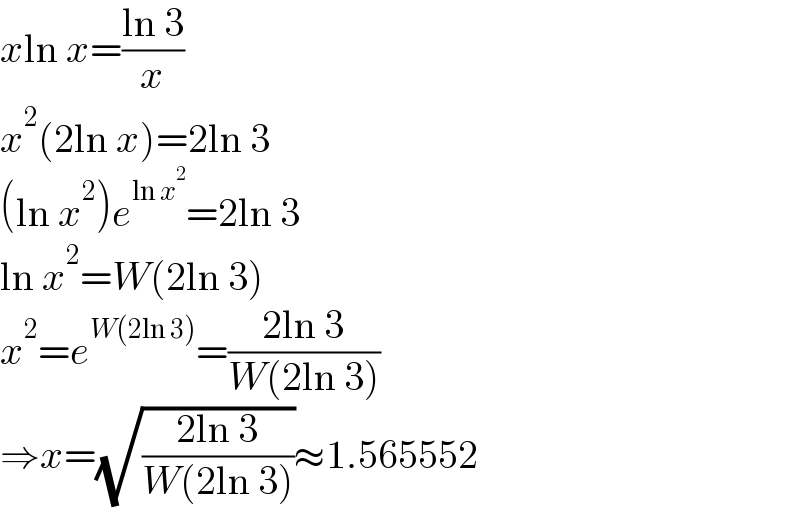
$${x}\mathrm{ln}\:{x}=\frac{\mathrm{ln}\:\mathrm{3}}{{x}} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{2ln}\:{x}\right)=\mathrm{2ln}\:\mathrm{3} \\ $$$$\left(\mathrm{ln}\:{x}^{\mathrm{2}} \right){e}^{\mathrm{ln}\:{x}^{\mathrm{2}} } =\mathrm{2ln}\:\mathrm{3} \\ $$$$\mathrm{ln}\:{x}^{\mathrm{2}} ={W}\left(\mathrm{2ln}\:\mathrm{3}\right) \\ $$$${x}^{\mathrm{2}} ={e}^{{W}\left(\mathrm{2ln}\:\mathrm{3}\right)} =\frac{\mathrm{2ln}\:\mathrm{3}}{{W}\left(\mathrm{2ln}\:\mathrm{3}\right)} \\ $$$$\Rightarrow{x}=\sqrt{\frac{\mathrm{2ln}\:\mathrm{3}}{{W}\left(\mathrm{2ln}\:\mathrm{3}\right)}}\approx\mathrm{1}.\mathrm{565552} \\ $$
Commented by Tawa11 last updated on 25/Jun/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
