Question Number 88771 by M±th+et£s last updated on 12/Apr/20

$${solve} \\ $$$${x}^{{x}^{\mathrm{4}} } =\mathrm{64} \\ $$
Commented by mr W last updated on 12/Apr/20
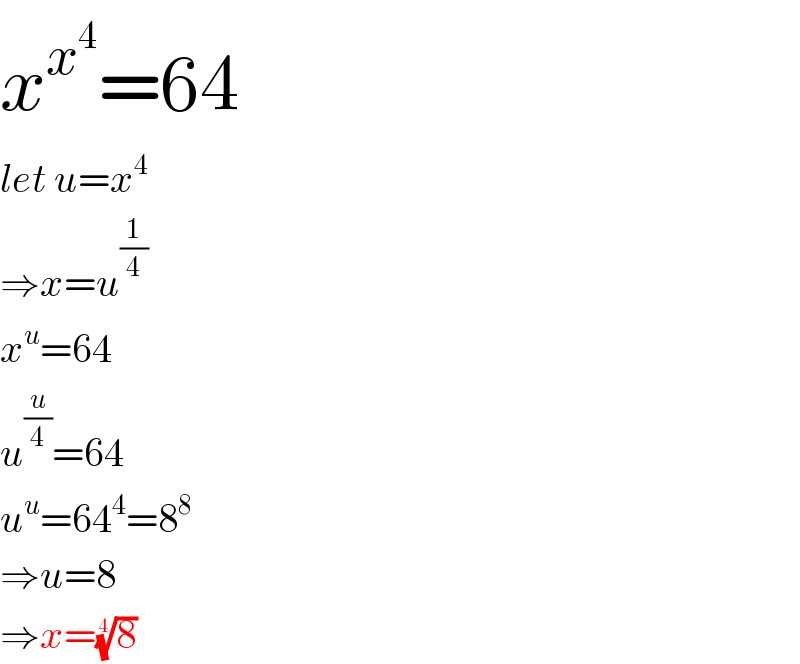
$${x}^{{x}^{\mathrm{4}} } =\mathrm{64} \\ $$$${let}\:{u}={x}^{\mathrm{4}} \\ $$$$\Rightarrow{x}={u}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${x}^{{u}} =\mathrm{64} \\ $$$${u}^{\frac{{u}}{\mathrm{4}}} =\mathrm{64} \\ $$$${u}^{{u}} =\mathrm{64}^{\mathrm{4}} =\mathrm{8}^{\mathrm{8}} \\ $$$$\Rightarrow{u}=\mathrm{8} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{4}}]{\mathrm{8}} \\ $$
Commented by mr W last updated on 12/Apr/20

$${yes}. \\ $$
Commented by M±th+et£s last updated on 12/Apr/20

$${i}\:{think}\:{its}\:\sqrt[{\mathrm{4}}]{\mathrm{8}} \\ $$
Commented by M±th+et£s last updated on 12/Apr/20
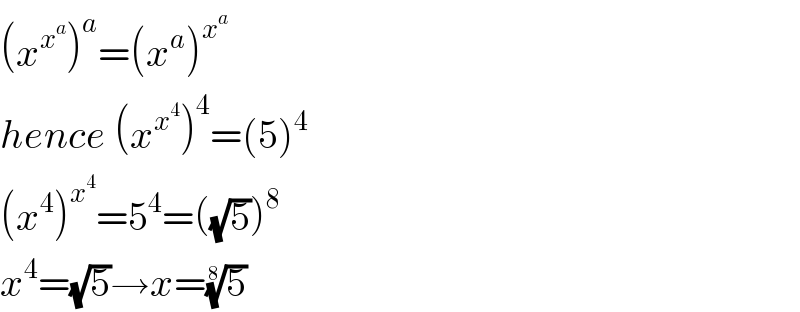
$$\left({x}^{{x}^{{a}} } \right)^{{a}} =\left({x}^{{a}} \right)^{{x}^{{a}} } \\ $$$${hence}\:\left({x}^{{x}^{\mathrm{4}} } \right)^{\mathrm{4}} =\left(\mathrm{5}\right)^{\mathrm{4}} \\ $$$$\left({x}^{\mathrm{4}} \right)^{{x}^{\mathrm{4}} } =\mathrm{5}^{\mathrm{4}} =\left(\sqrt{\mathrm{5}}\right)^{\mathrm{8}} \\ $$$${x}^{\mathrm{4}} =\sqrt{\mathrm{5}}\rightarrow{x}=\sqrt[{\mathrm{8}}]{\mathrm{5}} \\ $$
