Question Number 58622 by mr W last updated on 26/Apr/19

$${solve} \\ $$$${x}+{y}=\mathrm{2}{xy} \\ $$$${y}+{z}=\mathrm{3}{yz} \\ $$$${z}+{x}=\mathrm{7}{zx} \\ $$
Commented by rahul 19 last updated on 26/Apr/19

$${x}={y}={z}=\mathrm{0}\:. \\ $$
Commented by mr W last updated on 26/Apr/19

$${thanks}! \\ $$
Answered by tanmay last updated on 26/Apr/19
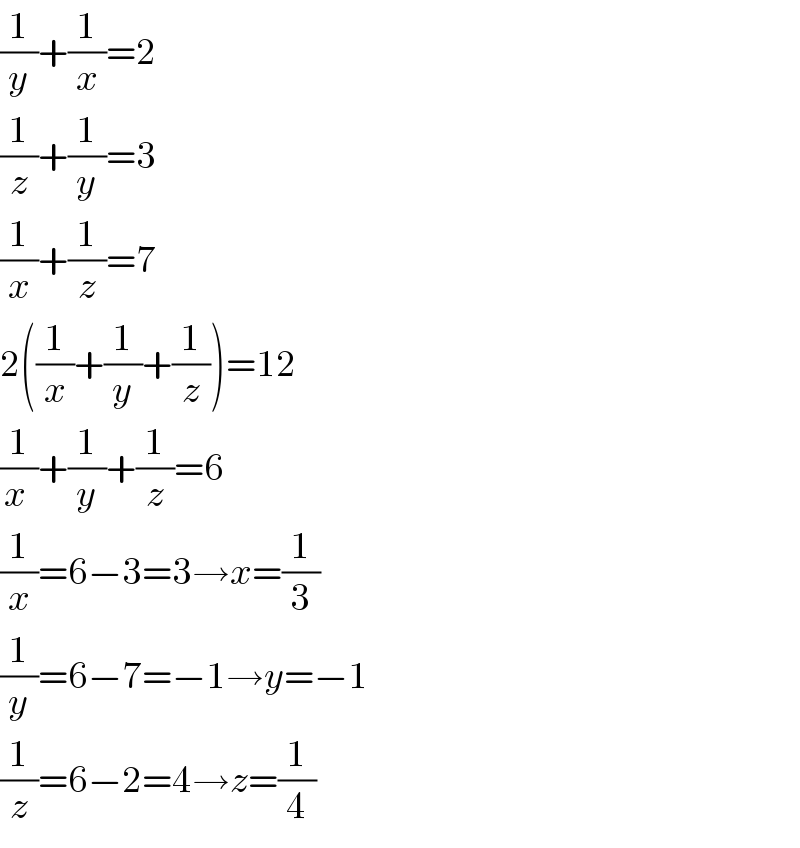
$$\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{x}}=\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{y}}=\mathrm{3} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{z}}=\mathrm{7} \\ $$$$\mathrm{2}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{12} \\ $$$$\frac{\mathrm{1}}{{x}\:}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\mathrm{6} \\ $$$$\frac{\mathrm{1}}{{x}}=\mathrm{6}−\mathrm{3}=\mathrm{3}\rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{{y}}=\mathrm{6}−\mathrm{7}=−\mathrm{1}\rightarrow{y}=−\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{z}}=\mathrm{6}−\mathrm{2}=\mathrm{4}\rightarrow{z}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 26/Apr/19
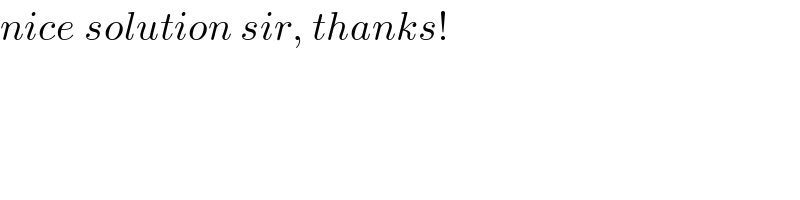
$${nice}\:{solution}\:{sir},\:{thanks}! \\ $$
Commented by tanmay last updated on 27/Apr/19

$${most}\:{welcome}\:{sir}… \\ $$
