Menu Close

Solve-x-y-3-i-x-y-y-x-6-ii-

Tinku Tara 0 Comments
Pin




Question Number 95394 by I want to learn more last updated on 24/May/20
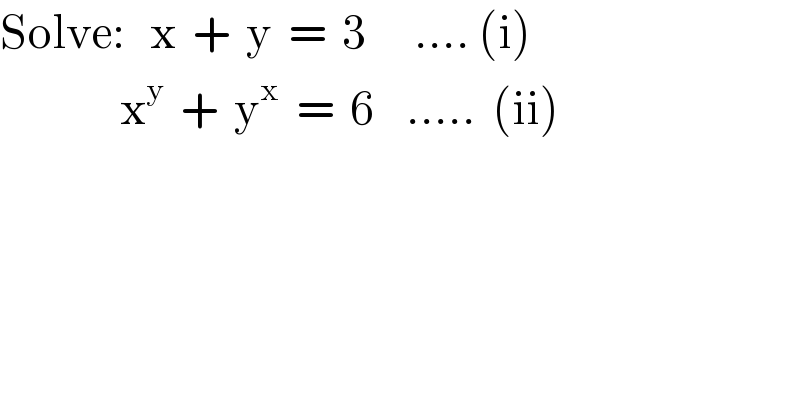
Solve: x + y = 3 .... (i) x^y + y^x = 6 ..... (ii)
$$\mathrm{Solve}:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:=\:\:\mathrm{3}\:\:\:\:\:\:….\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{y}} \:\:+\:\:\mathrm{y}^{\mathrm{x}} \:\:=\:\:\mathrm{6}\:\:\:\:…..\:\:\left(\mathrm{ii}\right) \\ $$
Commented by mr W last updated on 25/May/20
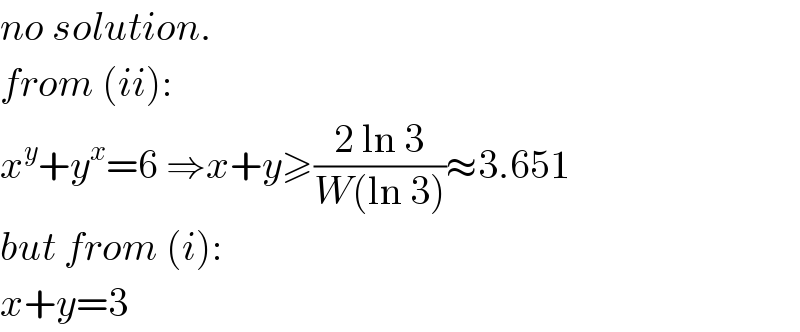
no solution. from (ii): x^y +y^x =6 ⇒x+y≥((2 ln 3)/(W(ln 3)))≈3.651 but from (i): x+y=3
$${no}\:{solution}. \\ $$$${from}\:\left({ii}\right): \\ $$$${x}^{{y}} +{y}^{{x}} =\mathrm{6}\:\Rightarrow{x}+{y}\geqslant\frac{\mathrm{2}\:\mathrm{ln}\:\mathrm{3}}{{W}\left(\mathrm{ln}\:\mathrm{3}\right)}\approx\mathrm{3}.\mathrm{651} \\ $$$${but}\:{from}\:\left({i}\right): \\ $$$${x}+{y}=\mathrm{3} \\ $$
Commented by I want to learn more last updated on 25/May/20
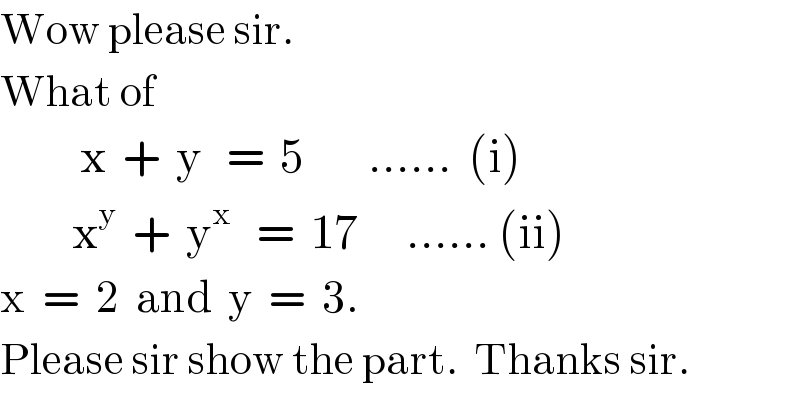
Wow please sir. What of x + y = 5 ...... (i) x^y + y^x = 17 ...... (ii) x = 2 and y = 3. Please sir show the part. Thanks sir.
$$\mathrm{Wow}\:\mathrm{please}\:\mathrm{sir}. \\ $$$$\mathrm{What}\:\mathrm{of} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:\:=\:\:\mathrm{5}\:\:\:\:\:\:\:\:……\:\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{y}} \:\:+\:\:\mathrm{y}^{\mathrm{x}} \:\:\:=\:\:\mathrm{17}\:\:\:\:\:\:……\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{x}\:\:=\:\:\mathrm{2}\:\:\mathrm{and}\:\:\mathrm{y}\:\:=\:\:\mathrm{3}. \\ $$$$\mathrm{Please}\:\mathrm{sir}\:\mathrm{show}\:\mathrm{the}\:\mathrm{part}.\:\:\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 25/May/20
x+y≥((2 ln ((17)/2))/(W(((17)/2))))≈4.841 with x+y=5>4.841 there are two solutions: x=2,y=3 or x=3,y=2. in this case the solutions are obvious. we can not calculate them using a formula. for example for x+y=6 the solutions are no longer obvious. you can get them only approximately.
$${x}+{y}\geqslant\frac{\mathrm{2}\:\mathrm{ln}\:\frac{\mathrm{17}}{\mathrm{2}}}{{W}\left(\frac{\mathrm{17}}{\mathrm{2}}\right)}\approx\mathrm{4}.\mathrm{841} \\ $$$${with}\:{x}+{y}=\mathrm{5}>\mathrm{4}.\mathrm{841}\:{there}\:{are}\:{two} \\ $$$${solutions}:\:{x}=\mathrm{2},{y}=\mathrm{3}\:{or}\:{x}=\mathrm{3},{y}=\mathrm{2}. \\ $$$${in}\:{this}\:{case}\:{the}\:{solutions}\:{are}\:{obvious}. \\ $$$${we}\:{can}\:{not}\:{calculate}\:{them}\:{using}\:{a} \\ $$$${formula}.\:{for}\:{example}\:{for}\:{x}+{y}=\mathrm{6}\: \\ $$$${the}\:{solutions}\:{are}\:{no}\:{longer}\:{obvious}. \\ $$$${you}\:{can}\:{get}\:{them}\:{only}\:{approximately}. \\ $$
Commented by I want to learn more last updated on 25/May/20
Thanks sir. I appreciate.
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by I want to learn more last updated on 25/May/20
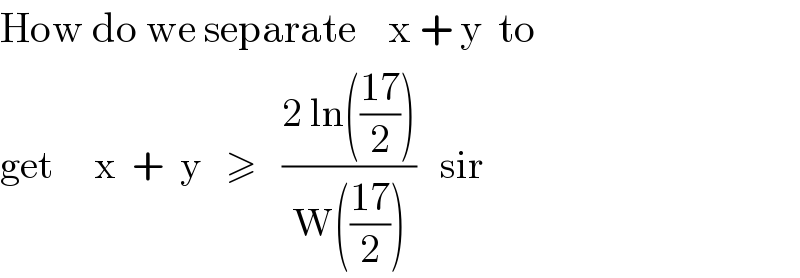
How do we separate x + y to get x + y ≥ ((2 ln(((17)/2)))/(W(((17)/2)))) sir
$$\mathrm{How}\:\mathrm{do}\:\mathrm{we}\:\mathrm{separate}\:\:\:\:\mathrm{x}\:+\:\mathrm{y}\:\:\mathrm{to} \\ $$$$\mathrm{get}\:\:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:\:\geqslant\:\:\:\frac{\mathrm{2}\:\mathrm{ln}\left(\frac{\mathrm{17}}{\mathrm{2}}\right)}{\mathrm{W}\left(\frac{\mathrm{17}}{\mathrm{2}}\right)}\:\:\:\mathrm{sir} \\ $$
Commented by I want to learn more last updated on 25/May/20
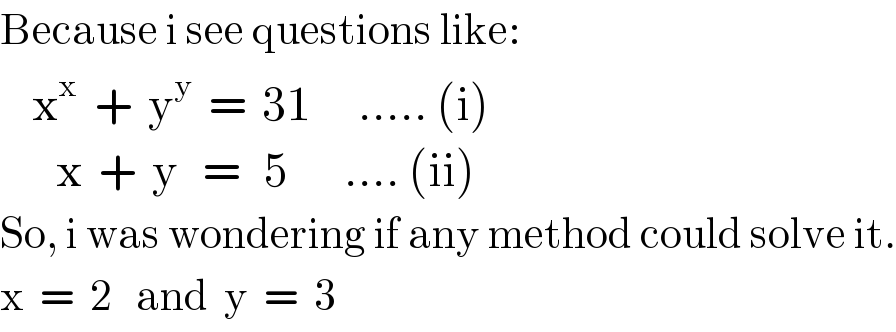
Because i see questions like: x^x + y^y = 31 ..... (i) x + y = 5 .... (ii) So, i was wondering if any method could solve it. x = 2 and y = 3
$$\mathrm{Because}\:\mathrm{i}\:\mathrm{see}\:\mathrm{questions}\:\mathrm{like}: \\ $$$$\:\:\:\:\mathrm{x}^{\mathrm{x}} \:\:+\:\:\mathrm{y}^{\mathrm{y}} \:\:=\:\:\mathrm{31}\:\:\:\:\:\:…..\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:\:=\:\:\:\mathrm{5}\:\:\:\:\:\:\:….\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{So},\:\mathrm{i}\:\mathrm{was}\:\mathrm{wondering}\:\mathrm{if}\:\mathrm{any}\:\mathrm{method}\:\mathrm{could}\:\mathrm{solve}\:\mathrm{it}. \\ $$$$\mathrm{x}\:\:=\:\:\mathrm{2}\:\:\:\mathrm{and}\:\:\mathrm{y}\:\:=\:\:\mathrm{3} \\ $$
Commented by mr W last updated on 25/May/20
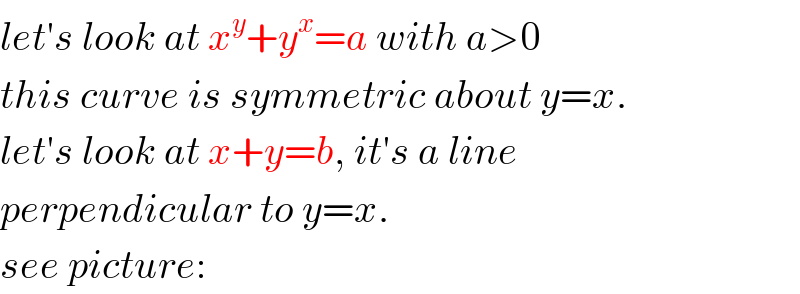
let′s look at x^y +y^x =a with a>0 this curve is symmetric about y=x. let′s look at x+y=b, it′s a line perpendicular to y=x. see picture:
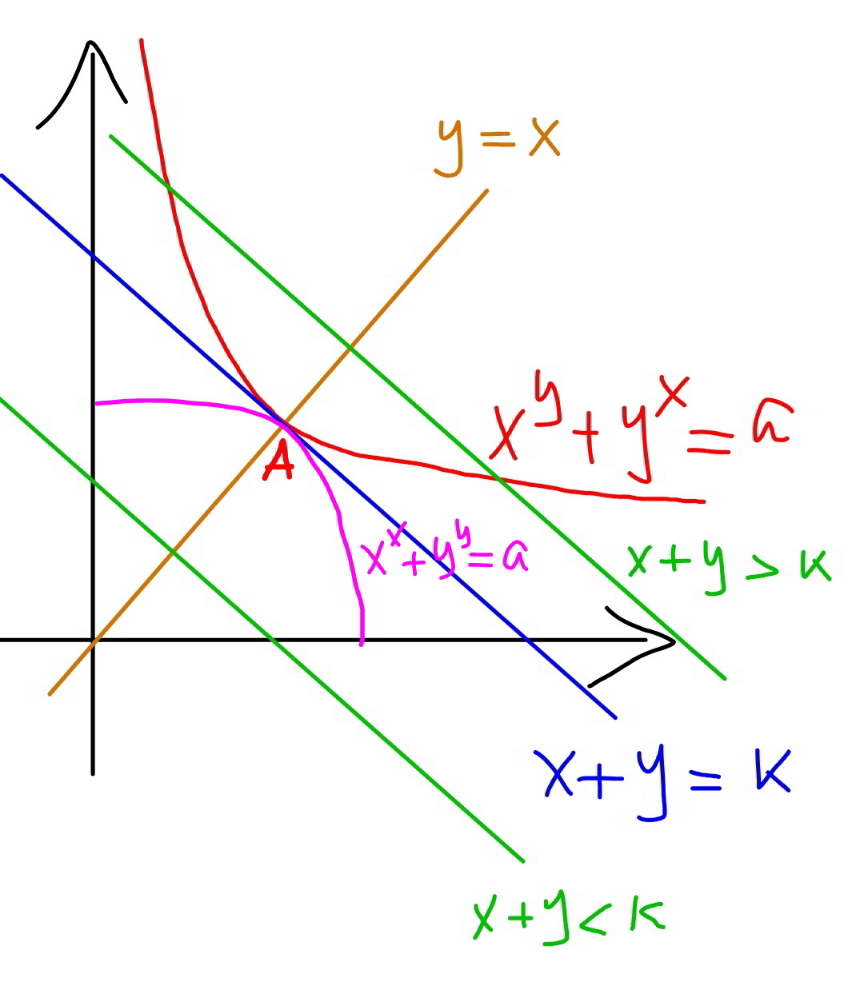
$${let}'{s}\:{look}\:{at}\:{x}^{{y}} +{y}^{{x}} ={a}\:{with}\:{a}>\mathrm{0} \\ $$$${this}\:{curve}\:{is}\:{symmetric}\:{about}\:{y}={x}. \\ $$$${let}'{s}\:{look}\:{at}\:{x}+{y}={b},\:{it}'{s}\:{a}\:{line}\: \\ $$$${perpendicular}\:{to}\:{y}={x}. \\ $$$${see}\:{picture}: \\ $$
Commented by mr W last updated on 25/May/20
Commented by I want to learn more last updated on 25/May/20
Thanks sir. I appreciate
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
Commented by mr W last updated on 25/May/20
we find a line x+y=k which tangents the curve x^y +y^x =a at point A. if x+y=b<k ⇒no solution. if x+y=b=k ⇒one solution. if x+y=b>k ⇒two solutions. say point A(p,p), we have p^p +p^p =a p^p =(a/2) ((ln ((a/2)))/p)e^((ln ((a/2)))/p) =ln ((a/2)) ⇒((ln ((a/2)))/p)=W(ln (a/2)) ⇒p=((ln (a/2))/(W(ln (a/2)))) line x+y=k passes through A(p,p) ⇒k=2p=((2 ln (a/2))/(W(ln (a/2))))
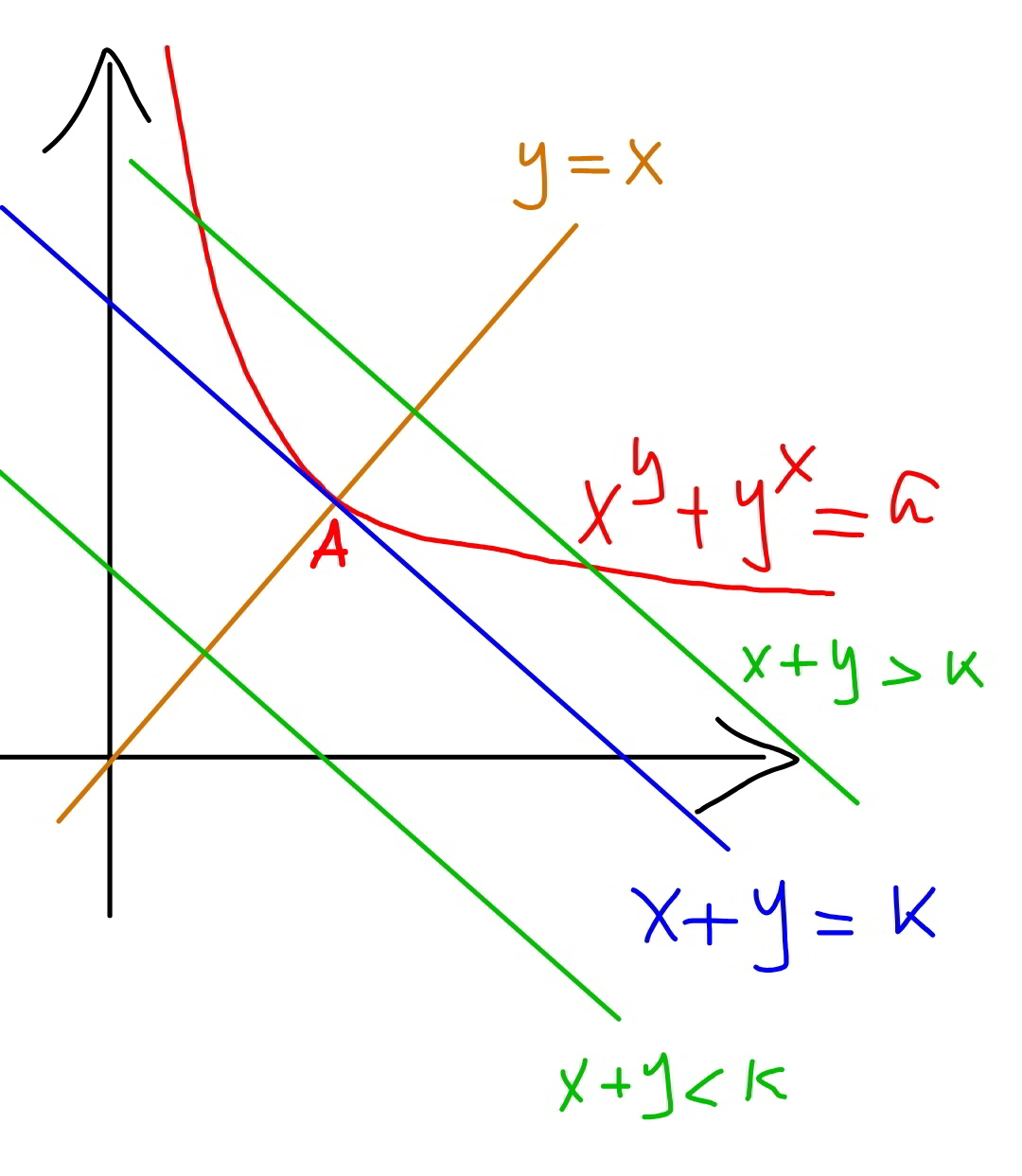
$${we}\:{find}\:{a}\:{line}\:{x}+{y}={k}\:{which}\:{tangents} \\ $$$${the}\:{curve}\:{x}^{{y}} +{y}^{{x}} ={a}\:{at}\:{point}\:{A}. \\ $$$${if}\:{x}+{y}={b}<{k}\:\Rightarrow{no}\:{solution}. \\ $$$${if}\:{x}+{y}={b}={k}\:\Rightarrow{one}\:{solution}. \\ $$$${if}\:{x}+{y}={b}>{k}\:\Rightarrow{two}\:{solutions}. \\ $$$$ \\ $$$${say}\:{point}\:{A}\left({p},{p}\right),\:{we}\:{have} \\ $$$${p}^{{p}} +{p}^{{p}} ={a} \\ $$$${p}^{{p}} =\frac{{a}}{\mathrm{2}} \\ $$$$\frac{\mathrm{ln}\:\left(\frac{{a}}{\mathrm{2}}\right)}{{p}}{e}^{\frac{\mathrm{ln}\:\left(\frac{{a}}{\mathrm{2}}\right)}{{p}}} =\mathrm{ln}\:\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\frac{\mathrm{ln}\:\left(\frac{{a}}{\mathrm{2}}\right)}{{p}}={W}\left(\mathrm{ln}\:\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{p}=\frac{\mathrm{ln}\:\frac{{a}}{\mathrm{2}}}{{W}\left(\mathrm{ln}\:\frac{{a}}{\mathrm{2}}\right)} \\ $$$${line}\:{x}+{y}={k}\:{passes}\:{through}\:{A}\left({p},{p}\right) \\ $$$$\Rightarrow{k}=\mathrm{2}{p}=\frac{\mathrm{2}\:\mathrm{ln}\:\frac{{a}}{\mathrm{2}}}{{W}\left(\mathrm{ln}\:\frac{{a}}{\mathrm{2}}\right)} \\ $$
Commented by I want to learn more last updated on 12/Dec/20
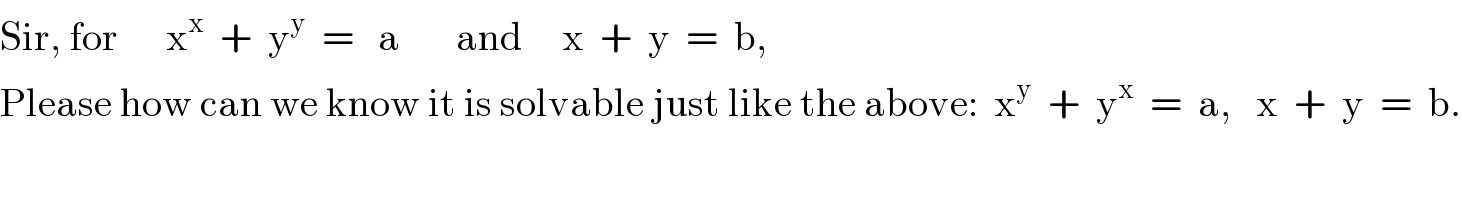
Sir, for x^x + y^y = a and x + y = b, Please how can we know it is solvable just like the above: x^y + y^x = a, x + y = b.
$$\mathrm{Sir},\:\mathrm{for}\:\:\:\:\:\:\mathrm{x}^{\mathrm{x}} \:\:+\:\:\mathrm{y}^{\mathrm{y}} \:\:=\:\:\:\mathrm{a}\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:=\:\:\mathrm{b}, \\ $$$$\mathrm{Please}\:\mathrm{how}\:\mathrm{can}\:\mathrm{we}\:\mathrm{know}\:\mathrm{it}\:\mathrm{is}\:\mathrm{solvable}\:\mathrm{just}\:\mathrm{like}\:\mathrm{the}\:\mathrm{above}:\:\:\mathrm{x}^{\mathrm{y}} \:\:+\:\:\mathrm{y}^{\mathrm{x}} \:\:=\:\:\mathrm{a},\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:=\:\:\mathrm{b}. \\ $$
Commented by I want to learn more last updated on 12/Dec/20
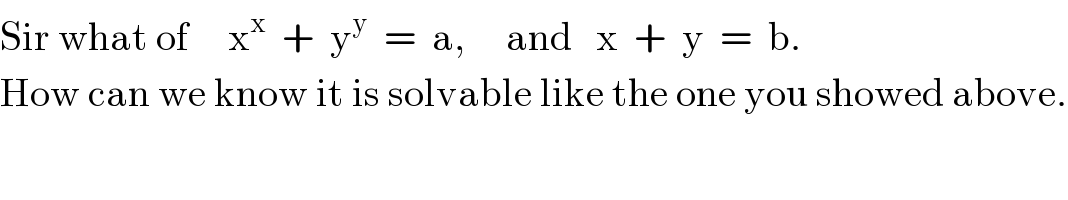
Sir what of x^x + y^y = a, and x + y = b. How can we know it is solvable like the one you showed above.
$$\mathrm{Sir}\:\mathrm{what}\:\mathrm{of}\:\:\:\:\:\mathrm{x}^{\mathrm{x}} \:\:+\:\:\mathrm{y}^{\mathrm{y}} \:\:=\:\:\mathrm{a},\:\:\:\:\:\mathrm{and}\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:=\:\:\mathrm{b}. \\ $$$$\mathrm{How}\:\mathrm{can}\:\mathrm{we}\:\mathrm{know}\:\mathrm{it}\:\mathrm{is}\:\mathrm{solvable}\:\mathrm{like}\:\mathrm{the}\:\mathrm{one}\:\mathrm{you}\:\mathrm{showed}\:\mathrm{above}. \\ $$
Commented by mr W last updated on 12/Dec/20
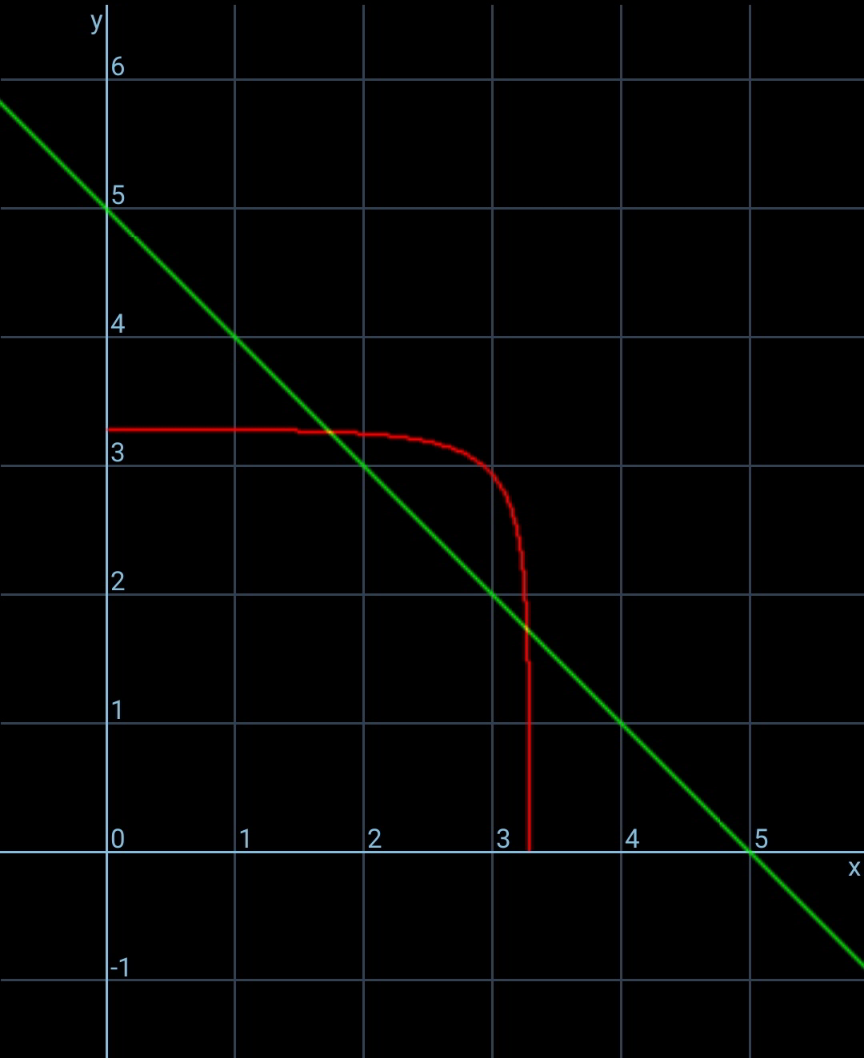
Commented by I want to learn more last updated on 12/Dec/20
Commented by I want to learn more last updated on 12/Dec/20
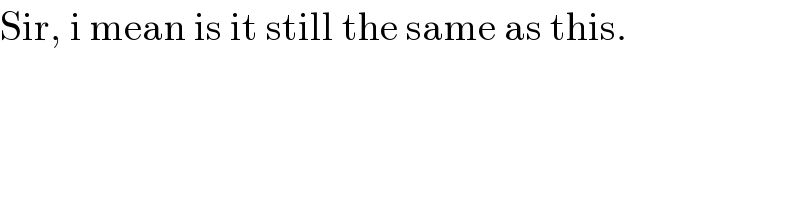
Sir, i mean is it still the same as this.
$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{mean}\:\mathrm{is}\:\mathrm{it}\:\mathrm{still}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{this}. \\ $$
Commented by mr W last updated on 12/Dec/20
you can proceed in similary way, but not exactly the same way.
$${you}\:{can}\:{proceed}\:{in}\:{similary}\:{way},\:{but} \\ $$$${not}\:{exactly}\:{the}\:{same}\:{way}. \\ $$
Commented by I want to learn more last updated on 13/Dec/20
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 13/Dec/20
Sir, i will really love it if you can show me sir. Am sorry to be taking your time. Please help me sir.
$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{will}\:\mathrm{really}\:\mathrm{love}\:\mathrm{it}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{show}\:\mathrm{me}\:\mathrm{sir}. \\ $$$$\mathrm{Am}\:\mathrm{sorry}\:\mathrm{to}\:\mathrm{be}\:\mathrm{taking}\:\mathrm{your}\:\mathrm{time}.\:\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 19/Jul/21
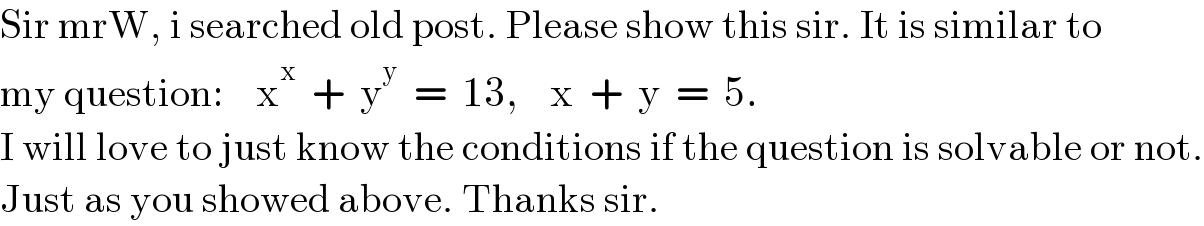
Sir mrW, i searched old post. Please show this sir. It is similar to my question: x^x + y^y = 13, x + y = 5. I will love to just know the conditions if the question is solvable or not. Just as you showed above. Thanks sir.
$$\mathrm{Sir}\:\mathrm{mrW},\:\mathrm{i}\:\mathrm{searched}\:\mathrm{old}\:\mathrm{post}.\:\mathrm{Please}\:\mathrm{show}\:\mathrm{this}\:\mathrm{sir}.\:\mathrm{It}\:\mathrm{is}\:\mathrm{similar}\:\mathrm{to} \\ $$$$\mathrm{my}\:\mathrm{question}:\:\:\:\:\mathrm{x}^{\mathrm{x}} \:\:+\:\:\mathrm{y}^{\mathrm{y}} \:\:=\:\:\mathrm{13},\:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:=\:\:\mathrm{5}. \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{love}\:\mathrm{to}\:\mathrm{just}\:\mathrm{know}\:\mathrm{the}\:\mathrm{conditions}\:\mathrm{if}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{solvable}\:\mathrm{or}\:\mathrm{not}. \\ $$$$\mathrm{Just}\:\mathrm{as}\:\mathrm{you}\:\mathrm{showed}\:\mathrm{above}.\:\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 20/Jul/21
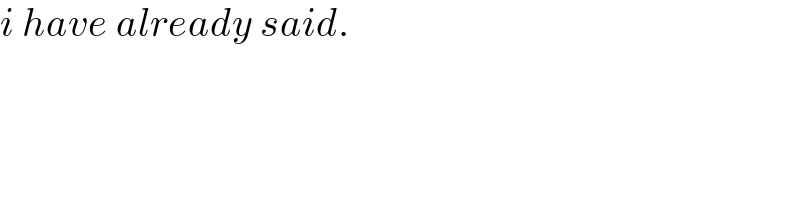
i have already said.
$${i}\:{have}\:{already}\:{said}. \\ $$
Commented by mr W last updated on 20/Jul/21
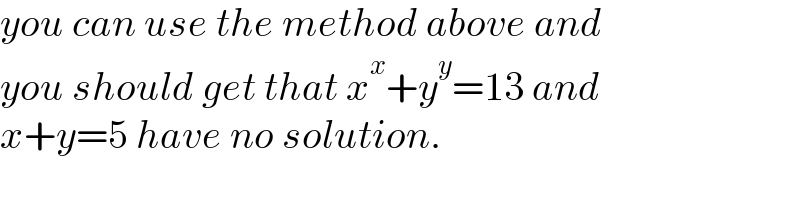
you can use the method above and you should get that x^x +y^y =13 and x+y=5 have no solution.
$${you}\:{can}\:{use}\:{the}\:{method}\:{above}\:{and} \\ $$$${you}\:{should}\:{get}\:{that}\:{x}^{{x}} +{y}^{{y}} =\mathrm{13}\:{and} \\ $$$${x}+{y}=\mathrm{5}\:{have}\:{no}\:{solution}. \\ $$
Commented by Tawa11 last updated on 20/Jul/21
I will try sir.
$$\mathrm{I}\:\mathrm{will}\:\mathrm{try}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 20/Jul/21
Thanks God bless you.
$$\mathrm{Thanks}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by Tawa11 last updated on 25/Jul/21
Sir, please help me. I am not getting it. Please.
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{it}.\:\:\mathrm{Please}. \\ $$
Commented by Tawa11 last updated on 25/Jul/21
Please!!!
$$\mathrm{Please}!!! \\ $$
Commented by mr W last updated on 25/Jul/21
i have said all what i can say and what i know. you know the graph of x^y +y^x =a and that for x^x +y^y =a and you know when the line x+y=b intersects these graphes and then get if there is a solution or two solutions or no solution. i put all this in following diagram:
$${i}\:{have}\:{said}\:{all}\:{what}\:{i}\:{can}\:{say}\:{and}\:{what} \\ $$$${i}\:{know}.\:{you}\:{know}\:{the}\:{graph}\:{of} \\ $$$${x}^{{y}} +{y}^{{x}} ={a}\:{and}\:{that}\:{for}\:{x}^{{x}} +{y}^{{y}} ={a}\:{and} \\ $$$${you}\:{know}\:{when}\:{the}\:{line}\:{x}+{y}={b}\: \\ $$$${intersects}\:{these}\:{graphes}\:{and}\:{then} \\ $$$${get}\:{if}\:{there}\:{is}\:{a}\:{solution}\:{or}\:{two} \\ $$$${solutions}\:{or}\:{no}\:{solution}.\:{i}\:{put}\:{all} \\ $$$${this}\:{in}\:{following}\:{diagram}: \\ $$
Commented by mr W last updated on 25/Jul/21
Commented by mr W last updated on 25/Jul/21
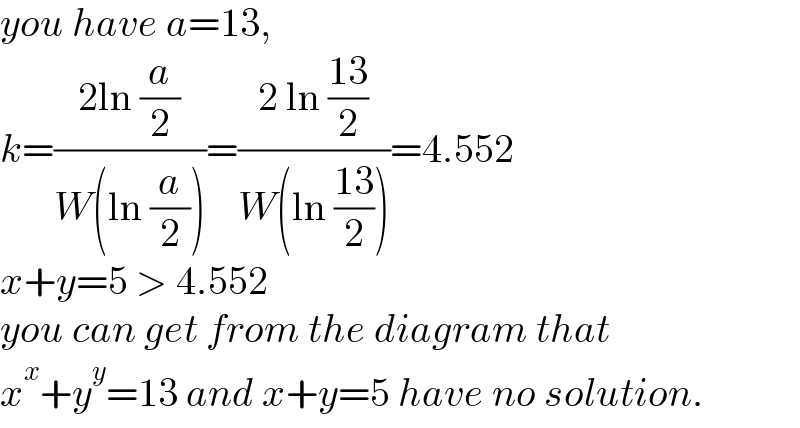
you have a=13, k=((2ln (a/2))/(W(ln (a/2))))=((2 ln ((13)/2))/(W(ln ((13)/2))))=4.552 x+y=5 > 4.552 you can get from the diagram that x^x +y^y =13 and x+y=5 have no solution.
$${you}\:{have}\:{a}=\mathrm{13}, \\ $$$${k}=\frac{\mathrm{2ln}\:\frac{{a}}{\mathrm{2}}}{{W}\left(\mathrm{ln}\:\frac{{a}}{\mathrm{2}}\right)}=\frac{\mathrm{2}\:\mathrm{ln}\:\frac{\mathrm{13}}{\mathrm{2}}}{{W}\left(\mathrm{ln}\:\frac{\mathrm{13}}{\mathrm{2}}\right)}=\mathrm{4}.\mathrm{552} \\ $$$${x}+{y}=\mathrm{5}\:>\:\mathrm{4}.\mathrm{552} \\ $$$${you}\:{can}\:{get}\:{from}\:{the}\:{diagram}\:{that} \\ $$$${x}^{{x}} +{y}^{{y}} =\mathrm{13}\:{and}\:{x}+{y}=\mathrm{5}\:{have}\:{no}\:{solution}. \\ $$
Commented by mr W last updated on 26/Jul/21
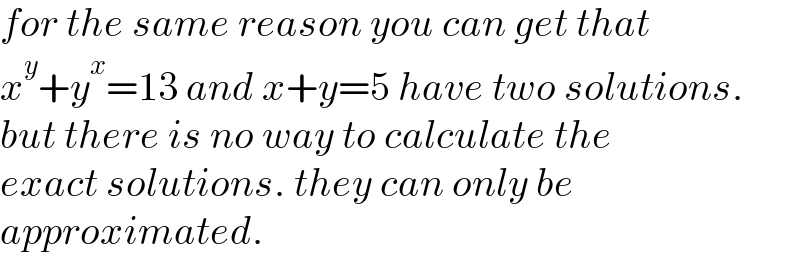
for the same reason you can get that x^y +y^x =13 and x+y=5 have two solutions. but there is no way to calculate the exact solutions. they can only be approximated.
$${for}\:{the}\:{same}\:{reason}\:{you}\:{can}\:{get}\:{that} \\ $$$${x}^{{y}} +{y}^{{x}} =\mathrm{13}\:{and}\:{x}+{y}=\mathrm{5}\:{have}\:{two}\:{solutions}. \\ $$$${but}\:{there}\:{is}\:{no}\:{way}\:{to}\:{calculate}\:{the} \\ $$$${exact}\:{solutions}.\:{they}\:{can}\:{only}\:{be} \\ $$$${approximated}. \\ $$
Commented by Tawa11 last updated on 26/Jul/21
God bless you sir. I really appreciate your time. Long life and good health and wealth.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}.\:\mathrm{Long}\:\mathrm{life}\:\mathrm{and}\:\mathrm{good}\:\mathrm{health} \\ $$$$\mathrm{and}\:\mathrm{wealth}. \\ $$
Commented by Tawa11 last updated on 09/Aug/21
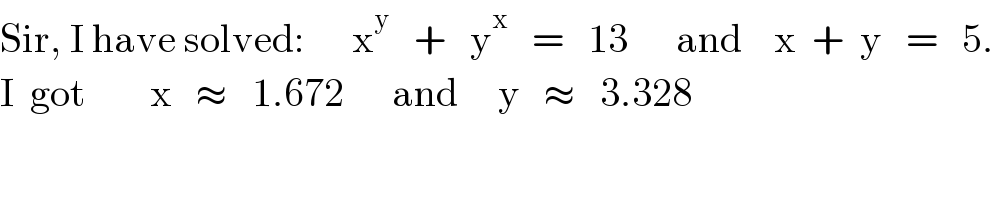
Sir, I have solved: x^y + y^x = 13 and x + y = 5. I got x ≈ 1.672 and y ≈ 3.328
$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{have}\:\mathrm{solved}:\:\:\:\:\:\:\mathrm{x}^{\mathrm{y}} \:\:\:+\:\:\:\mathrm{y}^{\mathrm{x}} \:\:\:=\:\:\:\mathrm{13}\:\:\:\:\:\:\mathrm{and}\:\:\:\:\mathrm{x}\:\:+\:\:\mathrm{y}\:\:\:=\:\:\:\mathrm{5}. \\ $$$$\mathrm{I}\:\:\mathrm{got}\:\:\:\:\:\:\:\:\mathrm{x}\:\:\:\approx\:\:\:\mathrm{1}.\mathrm{672}\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{y}\:\:\:\approx\:\:\:\mathrm{3}.\mathrm{328} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *