Question Number 173831 by dragan91 last updated on 19/Jul/22

$$\mathrm{Solve} \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{4} \\ $$$$\mathrm{x}^{\mathrm{x}} −\mathrm{y}^{\mathrm{y}} =\mathrm{13}\left(\mathrm{x}−\mathrm{y}\right) \\ $$
Answered by mr W last updated on 19/Jul/22

$${eqn}.\:\left(\mathrm{2}\right): \\ $$$${any}\:{x}={y}\:{is}\:{solution}. \\ $$$${eqn}.\:\left(\mathrm{1}\right): \\ $$$${x}+{y}=\mathrm{2}{x}=\mathrm{4} \\ $$$$\Rightarrow{x}={y}=\mathrm{2} \\ $$
Commented by dragan91 last updated on 19/Jul/22
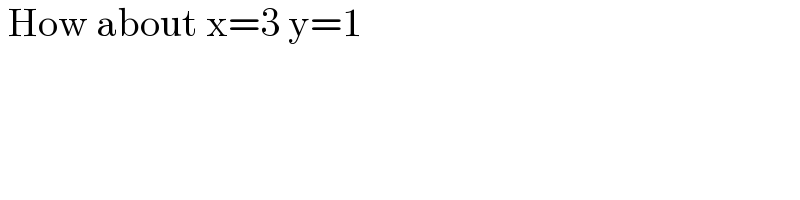
$$\:\mathrm{How}\:\mathrm{about}\:\mathrm{x}=\mathrm{3}\:\mathrm{y}=\mathrm{1} \\ $$
Commented by mr W last updated on 19/Jul/22
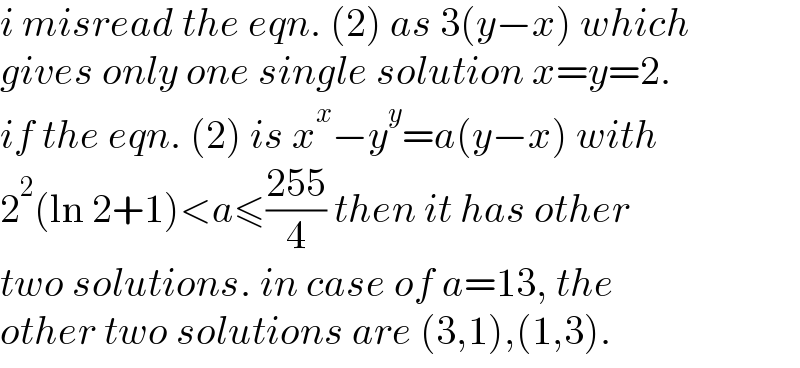
$${i}\:{misread}\:{the}\:{eqn}.\:\left(\mathrm{2}\right)\:{as}\:\mathrm{3}\left({y}−{x}\right)\:{which} \\ $$$${gives}\:{only}\:{one}\:{single}\:{solution}\:{x}={y}=\mathrm{2}. \\ $$$${if}\:{the}\:{eqn}.\:\left(\mathrm{2}\right)\:{is}\:{x}^{{x}} −{y}^{{y}} ={a}\left({y}−{x}\right)\:{with} \\ $$$$\mathrm{2}^{\mathrm{2}} \left(\mathrm{ln}\:\mathrm{2}+\mathrm{1}\right)<{a}\leqslant\frac{\mathrm{255}}{\mathrm{4}}\:{then}\:{it}\:{has}\:{other} \\ $$$${two}\:{solutions}.\:{in}\:{case}\:{of}\:{a}=\mathrm{13},\:{the} \\ $$$${other}\:{two}\:{solutions}\:{are}\:\left(\mathrm{3},\mathrm{1}\right),\left(\mathrm{1},\mathrm{3}\right). \\ $$
Commented by Tawa11 last updated on 19/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
