Menu Close

solve-xy-2-x-2-y-xe-x-2-

Tinku Tara 0 Comments
Pin




Question Number 98656 by mathmax by abdo last updated on 15/Jun/20
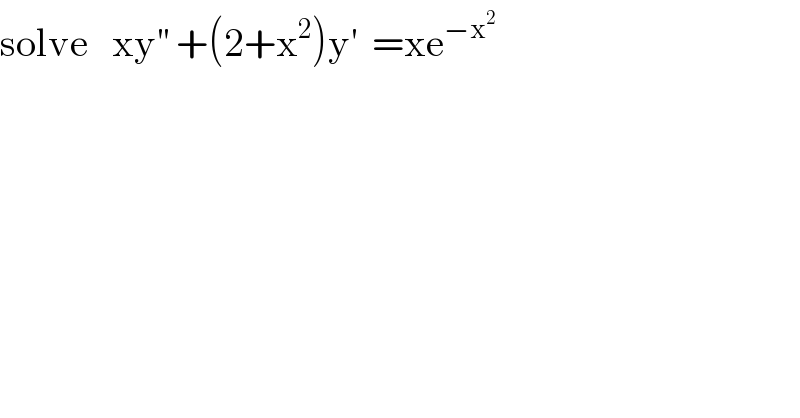
solve xy^(′′) +(2+x^2 )y^′ =xe^(−x^2 )
$$\mathrm{solve}\:\:\:\mathrm{xy}^{''} \:+\left(\mathrm{2}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{y}^{'} \:\:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \\ $$
Answered by MWSuSon last updated on 15/Jun/20
let y′′=p′ and y′=p xp′+(2+x^2 )p=xe^(−x^2 ) p′+(((2+x^2 ))/x)p=e^(−x^2 ) I.F=e^(∫(((2+x^2 ))/x)dx) =e^(lnx^2 +x^2 /2) =x^2 e^(x^2 /2) x^2 e^(x^2 /2) p′+(((2+x^2 ))/x)x^2 e^(x^2 /2) p=x^2 e^(−x^2 /2) (d/dx)(x^2 e^(x^2 /2) p)=x^2 e^(−x^2 /2) x^2 e^(x^2 /2) p=∫x^2 e^(−x^2 /2) dx x^2 e^(x^2 /2) p=(√(π/2))erf((x/( (√2))))−xe^(−x^2 /2) +c_1 p=(1/(x^2 e^(x^2 /2) ))[(√(π/2))erf((x/( (√2))))−xe^(−x^2 /2) +c_1 ] but p=y′ y=∫{(1/(x^2 e^(x^2 /2) ))[(√(π/2))erf((x/( (√2))))−xe^(−x^2 /2) +c_1 ]}dx
$${let}\:{y}''={p}'\:{and}\:{y}'={p} \\ $$$${xp}'+\left(\mathrm{2}+{x}^{\mathrm{2}} \right){p}={xe}^{−{x}^{\mathrm{2}} } \\ $$$${p}'+\frac{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)}{{x}}{p}={e}^{−{x}^{\mathrm{2}} } \\ $$$${I}.{F}={e}^{\int\frac{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)}{{x}}{dx}} ={e}^{{lnx}^{\mathrm{2}} +{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {p}'+\frac{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)}{{x}}{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {p}={x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$$\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {p}\right)={x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {p}=\int{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} /\mathrm{2}} {dx} \\ $$$${x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {p}=\sqrt{\frac{\pi}{\mathrm{2}}}{erf}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)−{xe}^{−{x}^{\mathrm{2}} /\mathrm{2}} +{c}_{\mathrm{1}} \\ $$$${p}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} }\left[\sqrt{\frac{\pi}{\mathrm{2}}}{erf}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)−{xe}^{−{x}^{\mathrm{2}} /\mathrm{2}} +{c}_{\mathrm{1}} \right] \\ $$$${but}\:{p}={y}' \\ $$$${y}=\int\left\{\frac{\mathrm{1}}{{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} }\left[\sqrt{\frac{\pi}{\mathrm{2}}}{erf}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)−{xe}^{−{x}^{\mathrm{2}} /\mathrm{2}} +{c}_{\mathrm{1}} \right]\right\}{dx} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 16/Jun/20
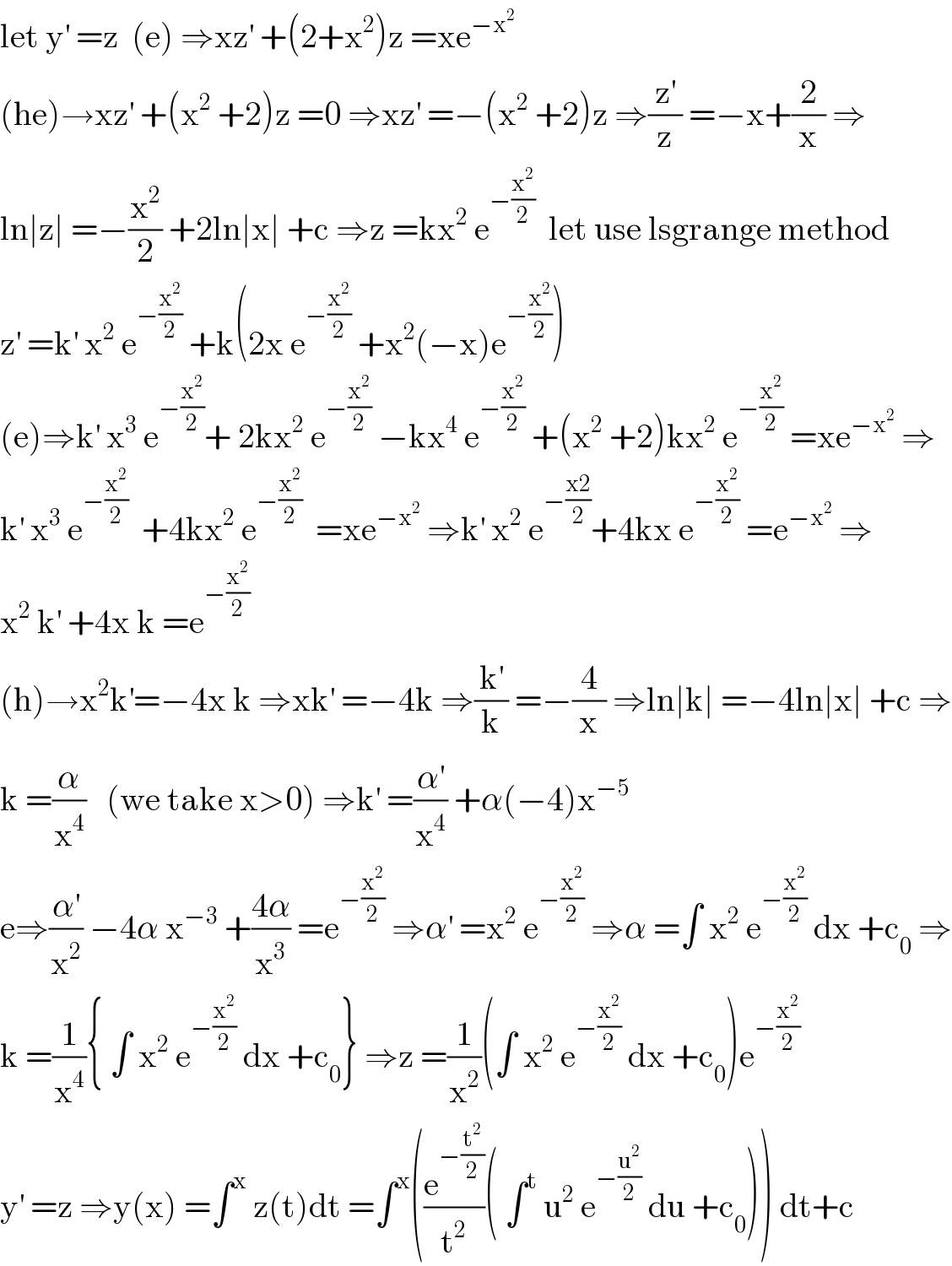
let y^′ =z (e) ⇒xz^′ +(2+x^2 )z =xe^(−x^2 ) (he)→xz^′ +(x^2 +2)z =0 ⇒xz^′ =−(x^2 +2)z ⇒(z^′ /z) =−x+(2/x) ⇒ ln∣z∣ =−(x^2 /2) +2ln∣x∣ +c ⇒z =kx^2 e^(−(x^2 /2)) let use lsgrange method z^′ =k^′ x^2 e^(−(x^2 /2)) +k(2x e^(−(x^2 /2)) +x^2 (−x)e^(−(x^2 /2)) ) (e)⇒k^′ x^3 e^(−(x^2 /2)) + 2kx^2 e^(−(x^2 /2)) −kx^4 e^(−(x^2 /2)) +(x^2 +2)kx^2 e^(−(x^2 /2)) =xe^(−x^2 ) ⇒ k^′ x^3 e^(−(x^2 /2)) +4kx^2 e^(−(x^2 /2)) =xe^(−x^2 ) ⇒k^′ x^2 e^(−((x2)/2)) +4kx e^(−(x^2 /2)) =e^(−x^2 ) ⇒ x^2 k^′ +4x k =e^(−(x^2 /2)) (h)→x^2 k^′ =−4x k ⇒xk^′ =−4k ⇒(k^′ /k) =−(4/x) ⇒ln∣k∣ =−4ln∣x∣ +c ⇒ k =(α/x^4 ) (we take x>0) ⇒k^′ =(α^′ /x^4 ) +α(−4)x^(−5) e⇒(α^′ /x^2 ) −4α x^(−3) +((4α)/x^3 ) =e^(−(x^2 /2)) ⇒α^′ =x^2 e^(−(x^2 /2)) ⇒α =∫ x^2 e^(−(x^2 /2)) dx +c_0 ⇒ k =(1/x^4 ){ ∫ x^2 e^(−(x^2 /2)) dx +c_0 } ⇒z =(1/x^2 )(∫ x^2 e^(−(x^2 /2)) dx +c_0 )e^(−(x^2 /2)) y^′ =z ⇒y(x) =∫^x z(t)dt =∫^x ((e^(−(t^2 /2)) /t^2 )( ∫^t u^2 e^(−(u^2 /2)) du +c_0 )) dt+c
$$\mathrm{let}\:\mathrm{y}^{'} \:=\mathrm{z}\:\:\left(\mathrm{e}\right)\:\Rightarrow\mathrm{xz}^{'} \:+\left(\mathrm{2}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{z}\:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{xz}^{'} \:+\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)\mathrm{z}\:=\mathrm{0}\:\Rightarrow\mathrm{xz}^{'} \:=−\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)\mathrm{z}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}\:=−\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{ln}\mid\mathrm{z}\mid\:=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{2ln}\mid\mathrm{x}\mid\:+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\mathrm{kx}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:\mathrm{let}\:\mathrm{use}\:\mathrm{lsgrange}\:\mathrm{method} \\ $$$$\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\mathrm{k}\left(\mathrm{2x}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\mathrm{x}^{\mathrm{2}} \left(−\mathrm{x}\right)\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \right) \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} +\:\mathrm{2kx}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:−\mathrm{kx}^{\mathrm{4}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)\mathrm{kx}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \:\Rightarrow \\ $$$$\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:+\mathrm{4kx}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \:\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x2}}{\mathrm{2}}} +\mathrm{4kx}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:=\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{k}^{'} \:+\mathrm{4x}\:\mathrm{k}\:=\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\left(\mathrm{h}\right)\rightarrow\mathrm{x}^{\mathrm{2}} \mathrm{k}^{'} =−\mathrm{4x}\:\mathrm{k}\:\Rightarrow\mathrm{xk}^{'} \:=−\mathrm{4k}\:\Rightarrow\frac{\mathrm{k}^{'} }{\mathrm{k}}\:=−\frac{\mathrm{4}}{\mathrm{x}}\:\Rightarrow\mathrm{ln}\mid\mathrm{k}\mid\:=−\mathrm{4ln}\mid\mathrm{x}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{k}\:=\frac{\alpha}{\mathrm{x}^{\mathrm{4}} }\:\:\:\left(\mathrm{we}\:\mathrm{take}\:\mathrm{x}>\mathrm{0}\right)\:\Rightarrow\mathrm{k}^{'} \:=\frac{\alpha^{'} }{\mathrm{x}^{\mathrm{4}} }\:+\alpha\left(−\mathrm{4}\right)\mathrm{x}^{−\mathrm{5}} \\ $$$$\mathrm{e}\Rightarrow\frac{\alpha^{'} }{\mathrm{x}^{\mathrm{2}} }\:−\mathrm{4}\alpha\:\mathrm{x}^{−\mathrm{3}} \:+\frac{\mathrm{4}\alpha}{\mathrm{x}^{\mathrm{3}} }\:=\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow\alpha^{'} \:=\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow\alpha\:=\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\mathrm{dx}\:+\mathrm{c}_{\mathrm{0}} \:\Rightarrow \\ $$$$\mathrm{k}\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\left\{\:\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\mathrm{dx}\:+\mathrm{c}_{\mathrm{0}} \right\}\:\Rightarrow\mathrm{z}\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\left(\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\mathrm{dx}\:+\mathrm{c}_{\mathrm{0}} \right)\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\int^{\mathrm{x}} \:\mathrm{z}\left(\mathrm{t}\right)\mathrm{dt}\:=\int^{\mathrm{x}} \left(\frac{\mathrm{e}^{−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{t}^{\mathrm{2}} }\left(\:\int^{\mathrm{t}} \:\mathrm{u}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}} \:\mathrm{du}\:+\mathrm{c}_{\mathrm{0}} \right)\right)\:\mathrm{dt}+\mathrm{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *