Question Number 38802 by tawa tawa last updated on 30/Jun/18

$$\mathrm{solve}:\:\:\:\mathrm{y}''\left(\mathrm{1}\:+\:\mathrm{4x}^{\mathrm{2}} \right)\:−\:\mathrm{8y}\:=\:\mathrm{0} \\ $$
Answered by MrW3 last updated on 30/Jun/18
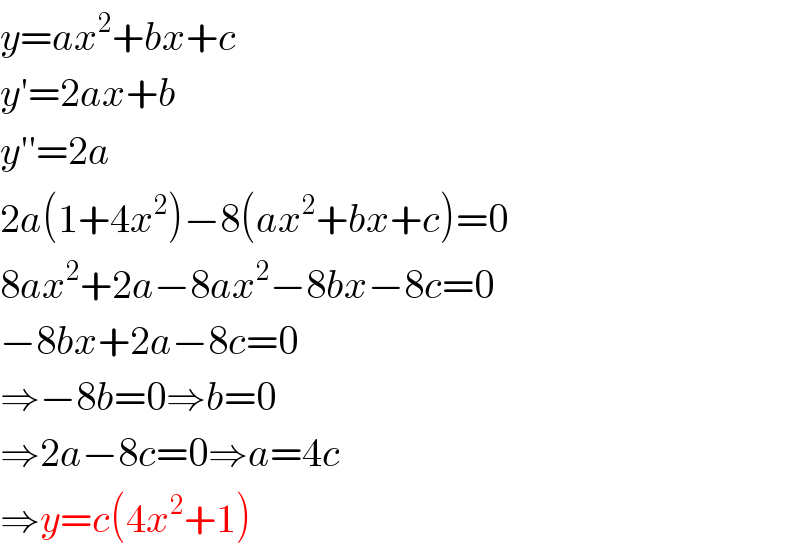
$${y}={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${y}'=\mathrm{2}{ax}+{b} \\ $$$${y}''=\mathrm{2}{a} \\ $$$$\mathrm{2}{a}\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)−\mathrm{8}\left({ax}^{\mathrm{2}} +{bx}+{c}\right)=\mathrm{0} \\ $$$$\mathrm{8}{ax}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{8}{ax}^{\mathrm{2}} −\mathrm{8}{bx}−\mathrm{8}{c}=\mathrm{0} \\ $$$$−\mathrm{8}{bx}+\mathrm{2}{a}−\mathrm{8}{c}=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{8}{b}=\mathrm{0}\Rightarrow{b}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{a}−\mathrm{8}{c}=\mathrm{0}\Rightarrow{a}=\mathrm{4}{c} \\ $$$$\Rightarrow{y}={c}\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$
Commented by tawa tawa last updated on 30/Jun/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Jun/18

$${y}={x}^{\alpha} +{h}\:{by}\:{trial}\:{method} \\ $$$${y}={x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\:{is}\:{a}\:{solution}… \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{x}\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{2} \\ $$$$\mathrm{2}\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)−\mathrm{8}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\boldsymbol{{S}}{O}\:{y}={x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\:\:{is}\:{the}\:{solution} \\ $$$${pls}\:{give}\:{me}\:{time}\:{to}\:{solve}\:{by}\:{standard}\:{method} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by tawa tawa last updated on 30/Jun/18

$$\mathrm{i}\:\mathrm{will}\:\mathrm{be}\:\mathrm{waiting}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
