Question Number 174367 by Mastermind last updated on 30/Jul/22
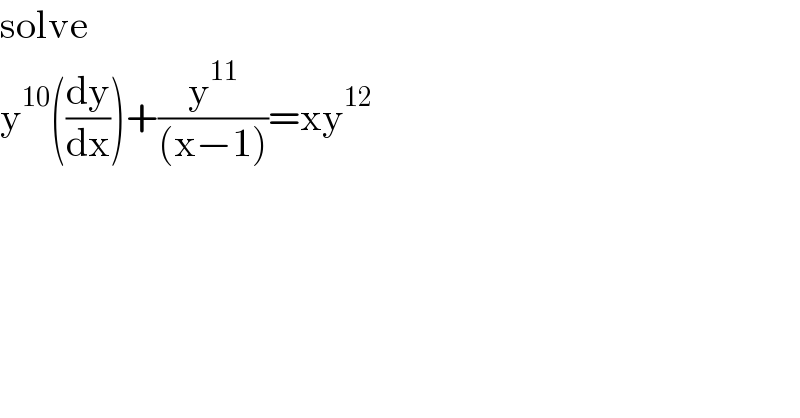
$$\mathrm{solve} \\ $$$$\mathrm{y}^{\mathrm{10}} \left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)+\frac{\mathrm{y}^{\mathrm{11}} }{\left(\mathrm{x}−\mathrm{1}\right)}=\mathrm{xy}^{\mathrm{12}} \\ $$
Commented by infinityaction last updated on 31/Jul/22
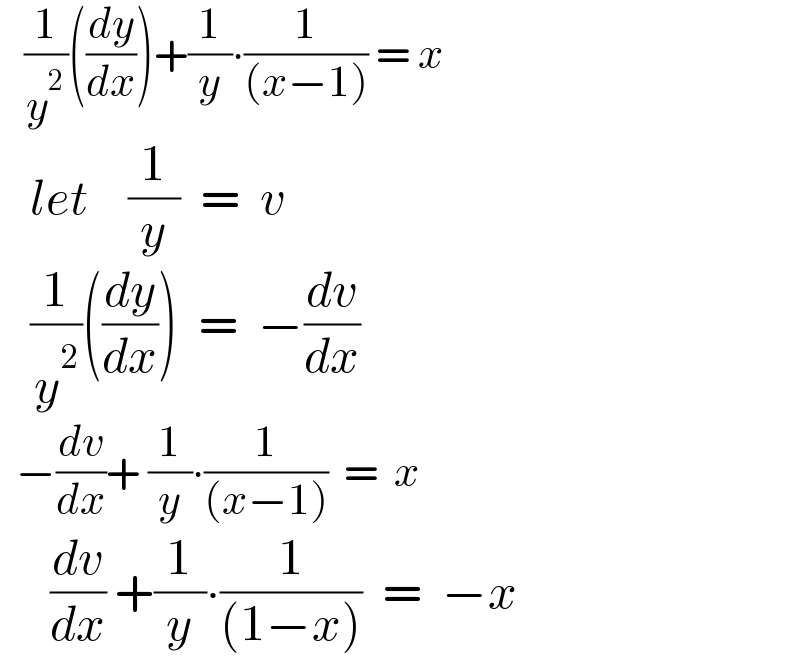
$$\:\:\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\left(\frac{{dy}}{{dx}}\right)+\frac{\mathrm{1}}{{y}}\centerdot\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)}\:=\:{x} \\ $$$$\:\:\:{let}\:\:\:\:\frac{\mathrm{1}}{{y}}\:\:=\:\:{v} \\ $$$$\:\:\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\left(\frac{{dy}}{{dx}}\right)\:\:=\:\:−\frac{{dv}}{{dx}} \\ $$$$\:\:−\frac{{dv}}{{dx}}+\:\frac{\mathrm{1}}{{y}}\centerdot\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)}\:\:=\:\:{x} \\ $$$$\:\:\:\:\:\frac{{dv}}{{dx}}\:+\frac{\mathrm{1}}{{y}}\centerdot\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)}\:\:=\:\:−{x} \\ $$
Commented by peter frank last updated on 01/Aug/22

$$\mathrm{thanks} \\ $$
